题目内容
11.在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上任取一个数x,则函数f(x)=sin2x的值不小于$\frac{1}{2}$的概率为( )| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{π}{3}$ |
分析 本题是几何概型的考查,利用区间长度的比即可求概率.
解答 解:∵函数f(x)=sin2x,
当x∈[-$\frac{π}{4}$,$\frac{π}{4}$]时,2x∈[-$\frac{π}{2}$,$\frac{π}{2}$],
函数f(x)=sin2x的值不小于$\frac{1}{2}$,则$\frac{π}{12}$≤x≤$\frac{π}{4}$,区间长度为$\frac{π}{6}$
则所求概率为P=$\frac{\frac{π}{6}}{\frac{π}{2}}$=$\frac{1}{3}$.
故选:B.
点评 本题考查了几何概型的概率求法;关键是正确选择测度比求概率.

练习册系列答案
相关题目
16.全称命题“?x∈R,x2+5x=4”的否定是( )
| A. | $?{x_0}∈R,{x_0}^2+5{x_0}=4$ | B. | ?x∈R,x2+5x≠4 | ||
| C. | $?{x_0}∈R,{x_0}^2+5{x_0}≠4$ | D. | 以上都不正确 |
3.圆x2+y2+2ax+4ay=0的半径为$\sqrt{5}$,则a等于( )
| A. | 5 | B. | -5或5 | C. | 1 | D. | 1或-1 |
20.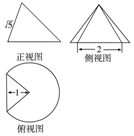 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )| A. | $π+\frac{2}{3}$ | B. | $π+\frac{1}{3}$ | C. | $\frac{3}{4}π+\frac{2}{3}$ | D. | $\frac{3}{4}π+\frac{1}{3}$ |
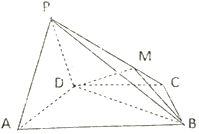 如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.
如图,在四棱锥P-ABCD中,平面PAD⊥平面ABCD,底面ABCD是一个梯形,且AB∥DC,△PAD是等边三角形,已知AD=4,BD=4$\sqrt{3}$,AD=2CD=8.