题目内容
1．袋中有大小形状相同的红球，黑球各一个，现依次有放回的随机摸去3次，每次摸取一球，若摸到红球时得2分，摸到黑球时得1分，则3次摸球所得总分为5的概率为$\frac{3}{8}$．分析 先求出基本事件总数为：n=23=8，再求出3次摸球所得总分为5包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{2}$=3，由此能求出3次摸球所得总分为5的概率．
解答 解：∵袋中有大小形状相同的红球，黑球各一个，
现依次有放回的随机摸去3次，每次摸取一球，
∴基本事件总数为：n=23=8，
∵摸到红球时得2分，摸到黑球时得1分，
∴3次摸球所得总分为5包含的基本事件个数m=${C}_{3}^{1}{C}_{2}^{2}$=3，
∴3次摸球所得总分为5的概率p=$\frac{3}{8}$．
故答案为：$\frac{3}{8}$．
点评 本题考查概率的求法，是基础题，解题时要认真审题，注意等可能事件概率计算公式的合理运用．
练习册系列答案
相关题目
11．在区间[-$\frac{π}{4}$，$\frac{π}{4}$]上任取一个数x，则函数f（x）=sin2x的值不小于$\frac{1}{2}$的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{π}{3}$ |
9．下列函数中，既是奇函数又是增函数的是（ ）
| A． | y=3x | B． | y=x2 | C． | y=lnx | D． | y=x|x| |
6．
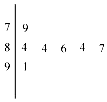某学校举行的演讲比赛有七位评委，如图是评委们为某选手给出分数的茎叶图，根据规则去掉一个最高分和一个最低分．则此所剩数据的平均数和方差分别为（ ）
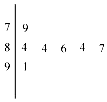某学校举行的演讲比赛有七位评委，如图是评委们为某选手给出分数的茎叶图，根据规则去掉一个最高分和一个最低分．则此所剩数据的平均数和方差分别为（ ）| A． | 84，4.84 | B． | 84，1.6 | C． | 85，4 | D． | 85，1.6 |
13．
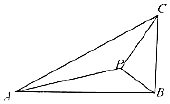如图所示，P为△ABC内一点，且满足△ABC∽△CPB，∠ABC=∠CPB=90°，$AB=2\sqrt{3}$，BC=2，则PA=（ ）
如图所示，P为△ABC内一点，且满足△ABC∽△CPB，∠ABC=∠CPB=90°，$AB=2\sqrt{3}$，BC=2，则PA=（ ）| A． | 7 | B． | $\sqrt{5}$ | C． | $\sqrt{7}$ | D． | $\sqrt{19}$ |
10．设集合A={-2，-1，0，1，2}，B={x|x2+2x＜0}，则A∩B=（ ）
| A． | {1，2} | B． | {-2，-1} | C． | {-1} | D． | {-2，-1，0} |
11．在△ABC中，A，B，C的对边分别为a，b，c，若2（a2+c2）-ac=2b2，则sinB=（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{15}}}{4}$ | D． | $\frac{{\sqrt{3}}}{2}$ |