题目内容
6.已知以F为焦点的抛物线y2=4x上的两点A、B满足$\overrightarrow{AF}=3\overrightarrow{FB}$,求|AB|=$\frac{16}{3}$.分析 设BF=m,由抛物线的定义知AA1和BB1,进而可推断出AC和AB,及直线AB的斜率,则直线AB的方程可得,与抛物线方程联立消去y,进而跟韦达定理求得x1+x2的值,则根据抛物线的定义求得弦AB的长度.
解答 解:设$|\overrightarrow{FB}|=m$,由$\overrightarrow{AF}=3\overrightarrow{FB}$,可得:$|\overrightarrow{FA}|$=3m,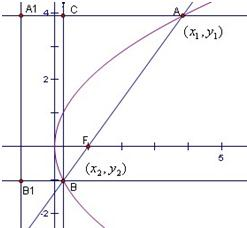
由抛物线的定义知AA1=3m,BB1=m,
∴△ABC中,AC=2m,AB=4m,kAB=$\sqrt{3}$,
∴直线AB方程为y=$\sqrt{3}$(x-1),
与抛物线方程联立消y得3x2-10x+3=0
所以|AB|=x1+x2+2=$\frac{16}{3}$,
故答案为:$\frac{16}{3}$.
点评 本题主要考查了抛物线的简单性质.考查了直线与抛物线的关系及焦点弦的问题.常需要利用抛物线的定义来解决.

练习册系列答案
相关题目
11.在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上任取一个数x,则函数f(x)=sin2x的值不小于$\frac{1}{2}$的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{π}{3}$ |
18.已知椭圆的焦点在y轴上,长轴长为10,短轴长为8,F1、F2为椭圆的左、右焦点.
(1)求椭圆的标准方程;
(2)求椭圆的焦点坐标、离心率;
(3)求以椭圆的焦点为顶点、顶点为焦点的双曲线的标准方程.
(1)求椭圆的标准方程;
(2)求椭圆的焦点坐标、离心率;
(3)求以椭圆的焦点为顶点、顶点为焦点的双曲线的标准方程.
15.已知集合$M=\left\{{\left.{({x,y})}\right|\left\{\begin{array}{l}2x+y=2\\ x-y=1\end{array}\right.}\right\}$,则( )
| A. | M={1,0} | B. | M={(1,0)} | C. | M=(1,0) | D. | M={1} |