题目内容
20.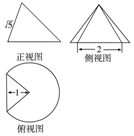 一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )
一个圆锥被过顶点的平面截去了较小的一部分,余下的几何体的三视图如图,则该几何体的体积为( )| A. | $π+\frac{2}{3}$ | B. | $π+\frac{1}{3}$ | C. | $\frac{3}{4}π+\frac{2}{3}$ | D. | $\frac{3}{4}π+\frac{1}{3}$ |
分析 由三视图可得:∠AOB=90°.该几何体的体积为:V=$\frac{3}{4}$V圆柱+V三棱锥P-AOB.
解答 解:由已知中的三视图,圆锥母线l=$\sqrt{(\sqrt{5})^{2}+{1}^{2}}$=$\sqrt{6}$,圆锥的高h=$\sqrt{5-1}$=2,
圆锥底面半径为r=$\sqrt{{1}^{2}+{1}^{2}}$=$\sqrt{2}$,∠AOB=90°.
故该几何体的体积为:V=$\frac{3}{4}$V圆柱+V三棱锥P-AOB
=$\frac{3}{4}×$$\frac{1}{3}$Sh+$\frac{1}{3}×\frac{1}{2}×2×1×2$=$\frac{3}{4}×$$\frac{1}{3}$×$π×(\sqrt{2})^{2}×2$+$\frac{2}{3}$=$π+\frac{2}{3}$,
故选:A.
点评 本题考查了圆锥与三棱锥的三视图的及其体积计算公式,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
11.在区间[-$\frac{π}{4}$,$\frac{π}{4}$]上任取一个数x,则函数f(x)=sin2x的值不小于$\frac{1}{2}$的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{π}{3}$ |
15.已知集合$M=\left\{{\left.{({x,y})}\right|\left\{\begin{array}{l}2x+y=2\\ x-y=1\end{array}\right.}\right\}$,则( )
| A. | M={1,0} | B. | M={(1,0)} | C. | M=(1,0) | D. | M={1} |
5.已知集合M={x|-1≤x<3,x∈R},N={-1,0,1,2,3},则M∩N=( )
| A. | {-1,0,2,3} | B. | {-1,0,1,2} | C. | {0,1,2} | D. | {0,1,2,3} |
9.下列函数中,既是奇函数又是增函数的是( )
| A. | y=3x | B. | y=x2 | C. | y=lnx | D. | y=x|x| |
10.设集合A={-2,-1,0,1,2},B={x|x2+2x<0},则A∩B=( )
| A. | {1,2} | B. | {-2,-1} | C. | {-1} | D. | {-2,-1,0} |