题目内容
16．全称命题“?x∈R，x2+5x=4”的否定是（ ）| A． | $?{x_0}∈R，{x_0}^2+5{x_0}=4$ | B． | ?x∈R，x2+5x≠4 | ||
| C． | $?{x_0}∈R，{x_0}^2+5{x_0}≠4$ | D． | 以上都不正确 |
分析 欲写出命题的否定，必须同时改变两个地方：①：“?”；②：“=”即可，据此分析选项可得答案．
解答 解：全称命题“?x∈R，x2+5x=4”的否定是：?x0∈R，x02+5x0≠4，
故选：C
点评 这类问题的常见错误是没有把全称量词改为存在量词，或者对于“=”的否定用“≠”了．这里就有注意量词的否定形式．如“都是”的否定是“不都是”，而不是“都不是”．特称命题的否定是全称命题，“存在”对应“任意”．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
6．双曲线$\frac{x^2}{9}-\frac{y^2}{16}=1$的左右焦点分别为F1，F2，P是双曲线上的点，且∠F1PF2=90°，则△F1PF2的面积S=（ ）
| A． | 12 | B． | 16 | C． | 20 | D． | 24 |
11．在区间[-$\frac{π}{4}$，$\frac{π}{4}$]上任取一个数x，则函数f（x）=sin2x的值不小于$\frac{1}{2}$的概率为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{1}{3}$ | C． | $\frac{2}{3}$ | D． | $\frac{π}{3}$ |
1．已知集合A={-1，1，2，3，4}，B={-2，-1，0，1，2}，则A∩B（ ）
| A． | {3，4} | B． | {-2，3} | C． | {-2，4} | D． | {-1，1，2} |
5．已知集合M={x|-1≤x＜3，x∈R}，N={-1，0，1，2，3}，则M∩N=（ ）
| A． | {-1，0，2，3} | B． | {-1，0，1，2} | C． | {0，1，2} | D． | {0，1，2，3} |
6．
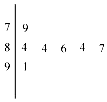某学校举行的演讲比赛有七位评委，如图是评委们为某选手给出分数的茎叶图，根据规则去掉一个最高分和一个最低分．则此所剩数据的平均数和方差分别为（ ）
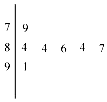某学校举行的演讲比赛有七位评委，如图是评委们为某选手给出分数的茎叶图，根据规则去掉一个最高分和一个最低分．则此所剩数据的平均数和方差分别为（ ）| A． | 84，4.84 | B． | 84，1.6 | C． | 85，4 | D． | 85，1.6 |