题目内容
已知函数f(x)=loga(2+x),g(x)=loga(2-x),a>0且a≠1且设h(x)=f(x)-g(x).
(Ⅰ)求函数h(x)的定义域;
(Ⅱ)判断h(x)的奇偶性,并加以证明;
(Ⅲ)当f(x)>g(x)时,求x的取值范围.
(Ⅰ)求函数h(x)的定义域;
(Ⅱ)判断h(x)的奇偶性,并加以证明;
(Ⅲ)当f(x)>g(x)时,求x的取值范围.
考点:函数奇偶性的判断,对数的运算性质
专题:函数的性质及应用
分析:(I)h(x)=f(x)-g(x)=loga(2+x)-loga(2-x),
要使函数h(x)有意义,可得
,解得即可.
(II)判断h(-x)与±h(x)的关系即可得出.
(III)loga(2+x)>loga(2-x).分类讨论:当0<a<1时,当1<a时,利用对数函数的单调性即可得出.
要使函数h(x)有意义,可得
|
(II)判断h(-x)与±h(x)的关系即可得出.
(III)loga(2+x)>loga(2-x).分类讨论:当0<a<1时,当1<a时,利用对数函数的单调性即可得出.
解答:
解:(I)h(x)=f(x)-g(x)=loga(2+x)-loga(2-x),
∴
,解得-2<x<2.
∴函数h(x)的定义域为(-2,2).
(II)∵h(-x)=loga(2-x)-loga(2+x)=-h(x),
∴函数h(x)为奇函数.
(III)∵f(x)>g(x),∴loga(2+x)>loga(2-x).
当0<a<1时,0<2+x<2-x,解得-2<x<0,即x的取值范围是(-2,0).
当1<a时,2+x>2-x>0,解得0<x<2,即x的取值范围是(0,2).
∴
|
∴函数h(x)的定义域为(-2,2).
(II)∵h(-x)=loga(2-x)-loga(2+x)=-h(x),
∴函数h(x)为奇函数.
(III)∵f(x)>g(x),∴loga(2+x)>loga(2-x).
当0<a<1时,0<2+x<2-x,解得-2<x<0,即x的取值范围是(-2,0).
当1<a时,2+x>2-x>0,解得0<x<2,即x的取值范围是(0,2).
点评:本题考查了对数函数类型函数的单调性、奇偶性、定义域,考查了计算能力,属于基础题.

练习册系列答案
相关题目
log3
=( )
| 3 |
| A、1 | ||
B、
| ||
C、-
| ||
| D、-2 |
已知函数f(x)=
,则f(-10)的值是( )
|
| A、-2 | B、-1 | C、0 | D、1 |
方程lnx=2-x的根所在区间是( )
| A、(-1,0) |
| B、(0,1) |
| C、(1,2) |
| D、(2,3) |
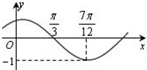 函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( )
函数f(x)=Acos(ωx+φ)(A>0,ω>0)的图象如图所示,为了得到g(x)=Acosωx的图象,可以将f(x)的图象( )A、向右平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向左平移
|
已知
=(-5,6),
=(6,5),则
与
( )
| a |
| b |
| a |
| b |
| A、垂直 | B、不垂直也不平行 |
| C、平行且同向 | D、平行且反向 |