题目内容
数列{an}的前n项和Sn=-
n2+kn(k∈N*),且Sn的最大值为8.
(1)确定常数k,求an;
(2)求Sn=|a1|+|a2|+|a3|+…+|an|(n∈N*)
(3)求数列{
}的前n项和Tn.
| 1 |
| 2 |
(1)确定常数k,求an;
(2)求Sn=|a1|+|a2|+|a3|+…+|an|(n∈N*)
(3)求数列{
| 9-2an |
| 2n |
考点:数列的求和,数列递推式
专题:等差数列与等比数列
分析:(1)利用二次函数的单调性、递推式的意义即可得出an.
(2)由题意得|an|=
.对n分类讨论,即可得出Sn.
(3)利用“错位相减法”、等比数列的前n项和公式即可得出.
(2)由题意得|an|=
|
(3)利用“错位相减法”、等比数列的前n项和公式即可得出.
解答:
解:(1)∵Sn=-
n2+kn=-
(n-k)2+
k2
∴当n=k时,Sn取得最大值.
∴
k2=8,解得k=4,此时Sn=-
n2+4n.
由
得an=-n+
(n≥2).
当n=1时,a1=S1=-
+4=
,符合上式,
∴an=-n+
.
(2)由题意,得|an|=
.
当1≤n≤4时,Sn=
=4n-
n2.
当n≥5时,Sn=4×4-
×42+
=
n2-4n+16.
∴Sn=
.
(3)∵bn=
=
,
∴Tn=1+
+
+…+
,
Tn=
+
+…+
+
,
两式向减可得,
Tn=1+
+
+
-
=
-
=2-
-
,
∴Tn=4-
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴当n=k时,Sn取得最大值.
∴
| 1 |
| 2 |
| 1 |
| 2 |
由
|
得an=-n+
| 9 |
| 2 |
当n=1时,a1=S1=-
| 1 |
| 2 |
| 7 |
| 2 |
∴an=-n+
| 9 |
| 2 |
(2)由题意,得|an|=
|
当1≤n≤4时,Sn=
n(
| ||||
| 2 |
| 1 |
| 2 |
当n≥5时,Sn=4×4-
| 1 |
| 2 |
(n-4)(
| ||||
| 2 |
=
| 1 |
| 2 |
∴Sn=
|
(3)∵bn=
| 9-2an |
| 2n |
| n |
| 2n-1 |
∴Tn=1+
| 2 |
| 2 |
| 3 |
| 22 |
| n |
| 2n-1 |
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 22 |
| n-1 |
| 2n-1 |
| n |
| 2n |
两式向减可得,
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 22 |
| 1 |
| 2n-1 |
| n |
| 2n |
1-
| ||
1-
|
| n |
| 2n |
| 1 |
| 2n-1 |
| n |
| 2n |
∴Tn=4-
| n+2 |
| 2n-1 |
点评:本题考查了二次函数的单调性、递推式的意义、分类讨论、“错位相减法”、等比数列的前n项和公式、含绝对值的数列求和问题,考查了推理能力与计算能力,属于难题.

练习册系列答案
相关题目
函数y=f(x)的部分图象如图所示,则y=f(x)的解析式为( )
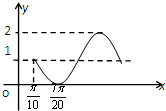

A、y=2sin(2x-
| ||
B、y=sin(2x-
| ||
C、y=2sin(2x+
| ||
D、y=sin(2x+
|
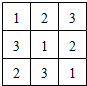 (1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).
(1)如图,将1,2,3填入3×3的方格中,要求每行、每列都没有重复数字,右面是一种填法,则不同的填写方法共有几种?(用数字作答).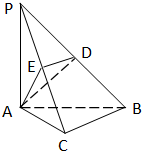 如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.
如图,在三棱锥P-ABC中,PA⊥底面ABC,PA=AB,∠ABC=60°,∠BCA=90°,点D、E分别是棱PB、PC的中点.