题目内容
下列说法中
①
=
②
=
③正数的n次方根有两个
④a的n次方根就是
⑤
=a
⑥(
)n=a
正确的个数为( )
①
| 12 | (-2)4 |
| 3 | -2 |
②
|
| 3 | 3 |
③正数的n次方根有两个
④a的n次方根就是
| n | a |
⑤
| n | an |
⑥(
| n | a |
正确的个数为( )
| A、1 | B、2 | C、3 | D、4 |
考点:方根与根式及根式的化简运算
专题:综合题
分析:把根式化为分数指数幂,根据幂的运算法则进行运算,结合乘方运算与开方运算之间的关系,对每一个命题进行判断即可.
解答:
解:对于①,
=2
=2
=
,∴①式错误;
对于②,
=(9
)
=32×
×
=3
=
,∴②式正确;
对于③,如
=3,∴命题③错误;
对于④,n为奇数时,a的n次方根是
,
n为偶数时,非负实数a的n次方根±
,∴命题④错误;
对于⑤,n为奇数时,
=a,n为偶数时,
=|a|,∴⑤错误;
对于⑥,根据乘方运算与开方运算是互为逆运算,知(
)n=a成立,∴⑥正确.
综上,正确的命题是②⑥.
故选:B.
| 12 | (-2)4 |
| 4 |
| 12 |
| 1 |
| 3 |
| 3 | 2 |
对于②,
|
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 3 | 3 |
对于③,如
| 3 | 27 |
对于④,n为奇数时,a的n次方根是
| n | a |
n为偶数时,非负实数a的n次方根±
| n | a |
对于⑤,n为奇数时,
| n | an |
| n | an |
对于⑥,根据乘方运算与开方运算是互为逆运算,知(
| n | a |
综上,正确的命题是②⑥.
故选:B.
点评:本题考查了根式与根式的化简与运算的问题,解题时应对每一个命题进行分析与判断,是基础题.

练习册系列答案
相关题目
右图是求x1,x2,…x10的乘积S的程序框图,图中空白框中应填入的内容为( )

| A、S=S*(n+1) |
| B、S=S*xn+1 |
| C、S=S*n |
| D、S=S*xn |
已知f(x)=10x-1-2,则f(x)的反函数当自变量取98时的函数值是( )
| A、1 | B、2 | C、3 | D、4 |
已知集合A={y|y=log2x,x>1},B={y|y=(
)x,x>1},则(∁RA)∪B=( )
| 1 |
| 2 |
A、{y|y<
| ||
| B、{y|y≤0或y>1} | ||
C、{y|
| ||
| D、R |
 如图,在?ABCD中,已知AB=2,AD=1,∠DAB=60°,M为DC的中点.
如图,在?ABCD中,已知AB=2,AD=1,∠DAB=60°,M为DC的中点.



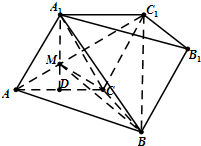 已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.
已知斜三棱柱ABC-A1B1C1中,四边形A1ACC1为菱形,∠ACB=90°,AC=BC=2,点D为AC的中点,A1D⊥平面ABC.