题目内容
已知O为△ABC内一点，且满足（
+
）⊥（
-
），（
+
）⊥（
-
），则O为△ABC的（ ）
| OA |
| OB |
| OA |
| OB |
| OB |
| OC |
| OB |
| OC |
| A、外心 | B、内心 | C、垂心 | D、重心 |
考点：数量积判断两个平面向量的垂直关系
专题：平面向量及应用
分析：由已知条件利用向量垂直的性质得到|
|=|
|，|
|=|
|，由此利用三角形五心的性质能求出结果．
| OA |
| OB |
| OB |
| OC |
解答：
解：∵（
+
）⊥（
-
），
∴（
+
）•（
-
）=
2-
2=0，
即|
|=|
|，
∵（
+
）⊥（
-
），
∴（
+
）•（
-
）=
2-
2=0，
即|
|=|
|，
∵O为△ABC内一点，
∴O为△ABC的内心．
故选：B．
| OA |
| OB |
| OA |
| OB |
∴（
| OA |
| OB |
| OA |
| OB |
| OA |
| OB |
即|
| OA |
| OB |
∵（
| OB |
| OC |
| OB |
| OC |
∴（
| OB |
| OC |
| OB |
| OC |
| OB |
| OC |
即|
| OB |
| OC |
∵O为△ABC内一点，
∴O为△ABC的内心．
故选：B．
点评：本题考查三角形五心的判断，是基础题，解题时要认真审题，注意向量垂直的性质的合理运用．
练习册系列答案
星级口算天天练系列答案
芒果教辅达标测试卷系列答案
相关题目
命题“若x2＞1，则x＞1”，则它的逆命题、否命题、逆否命题中真命题的个数是（ ）
| A、0 | B、1 | C、2 | D、3 |
直线方程3x+2y-6=0的斜率为k，在y轴上的截距为b，则有（ ）
A、k=-
| ||
B、k=-
| ||
C、k=-
| ||
D、k=-
|
为了得到函数y=sin（3x+
）的图象，可以由函数y=sinx的图象（ ）
| π |
| 4 |
A、先向右平移
| ||||
B、先向左平移
| ||||
C、先将其横坐标缩短为原来的
| ||||
D、先将其横坐标缩短为原来的
|
下列函数中既是偶函数，又在（0，+∞）上是单调递增函数的是（ ）
| A、y=-x2+1 |
| B、y=|x|+1 |
| C、y=log2x+1 |
| D、y=x3 |
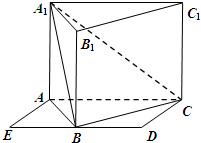如图，侧棱垂直于底面的三棱柱ABC-A1B1C1的底面ABC位于平行四边形ACDE中，AE=2，AA1=4，∠E=60°，点B为DE中点，AB⊥BC．