题目内容
已知集合A中只有1,x,x2+3x三个元素,且-2∈A,求实数x的值.
考点:元素与集合关系的判断
专题:集合
分析:由集合元素的互异性可得x≠1,且x≠x2+3x,根据元素与集合的关系可得:-2∈A时,x2+3x=-2,解得进而可得答案.
解答:
解:∵1,x,x2+3x,
∴x≠1,且x≠x2+3x,
即x≠0,x≠-2,x≠1,
∵-2∈A,
∴x2+3x=-2,
解得:x=-1,或x=-2(舍),
综上所述,x=-1.
∴x≠1,且x≠x2+3x,
即x≠0,x≠-2,x≠1,
∵-2∈A,
∴x2+3x=-2,
解得:x=-1,或x=-2(舍),
综上所述,x=-1.
点评:本题考查的知识点是集合元素的性质,正确理解集合元素的互异性是解答的关键.

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目
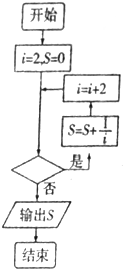 如图,给出的是计算
如图,给出的是计算| 1 |
| 2 |
| 1 |
| 4 |
| 1 |
| 6 |
| 1 |
| 2016 |
| A、i≤2021 |
| B、i≤2019 |
| C、i≤2017 |
| D、i≤2015 |
函数y=|sinx|的一个单调递增区间是( )
A、(
| ||
| B、(π,2π) | ||
C、(π,
| ||
| D、(0,π) |
斜率为3,在y轴上的截距为4的直线方程是( )
| A、3x-y+4=0 |
| B、x-3y-12=0 |
| C、3x-y-4=0 |
| D、3x-y-12=0 |
已知O为△ABC内一点,且满足(
+
)⊥(
-
),(
+
)⊥(
-
),则O为△ABC的( )
| OA |
| OB |
| OA |
| OB |
| OB |
| OC |
| OB |
| OC |
| A、外心 | B、内心 | C、垂心 | D、重心 |
 如图所示为函数f(x)=Asin(ωx+φ)( A>0,ω>0,0≤φ≤π)的部分图象,那么f(-3)=( )
如图所示为函数f(x)=Asin(ωx+φ)( A>0,ω>0,0≤φ≤π)的部分图象,那么f(-3)=( )A、-
| ||
| B、0 | ||
| C、-1 | ||
| D、1 |
已知非空数集 A={x∈R|x2=a},则实数a的取值范围为( )
| A、a=0 | B、a>0 |
| C、a≠0 | D、a≥0 |
复数
的值是( )
| 1 |
| 1+i |
A、-
| ||
B、
| ||
C、
| ||
D、
|