题目内容

设f（x）=
∫
x
0
sint
dt，则f′（x）=
 
．
考点：导数的运算
专题：导数的概念及应用
分析：根据牛莱公式求出f（x）的解析式，再根据导数公式求出f′（x）．
解答： 解：令G（t）=
sint
，G′（t）=f（t），
∴f（x）=
∫
x
0
sint
dt=
∫
x
0
g（t）dt=G（x）-G（0），
∴f′（x）=G′（x）-[G（0）]′=
sinx
，
故答案为：
sinx
，
点评：本题主要考查了积分和导数的求解公式，属于基本知识，基本运算．
练习册系列答案
相关题目
在△ABC中，已知a=4，b=4
3
，A=30°，B为锐角，那么角A，B，C的大小关系为（　　）
A、A＞B＞C
B、B＞A＞C
C、C＞B＞A
D、C＞A＞B
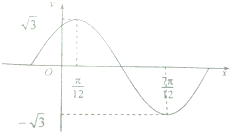已知函数f（x）=Asin（ωx+φ）（A＞0，ω＞0，0＜φ＜
π
2
）的部分图象如图：
（1）求函数f（x）的解析式及单调递增区间；
（2）将函数f（x）图象向右平移
π
6
个单位长度得到函数m（x）的图象，g（x）=2bcos2x（b＞0且b∈R），G（x）=m（x）+g（x），当x∈[0，
π
4
]时，求函数G（x）的值域．
已知f（x）=（
1
3
） x2-2x，g（x）=3x-6，求满足f（x）≥g（x）的x的取值范围．
已知f（x）=2ln（1+x）+ax2-2x+3（a＞0）
（1）求y=f（x）在（0，f（0））处的切线方程；
（2）求y=f（x）的单调区间．
已知sin（
π
4
-β）=-
12
13
，-
π
4
＜β＜
3π
4
，cos（α+
5π
4
）=
4
5
，
3π
4
＜α＜
7π
4
，求：
（1）sin2β；
（2）sin（α+β）．
如果函数y=Acos（2x+φ）（A＞0）的图象关于（
4π
3
，0）中心对称，那么φ的最小正值是
 
．
有以下几种说法：
①若两条直线平行，则它们的斜率相等；
②若两条直线的斜率之积为-1，则它们互相垂直；
③若直线l的倾斜角为θ，则该直线的斜率k=tanθ；
④直线l的方程为
2x
a2
+
y
b2
=-1（ab≠0），则该直线在y轴上的截距为-b2．
其中正确的说法的序号为
 
．
如图，正方体ABCD-A1B1C1D1的棱长为2．
（1）求异面直线BC1与B1D1所成的角；
（2）求三棱锥A1-AB1D1的体积．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网