题目内容
 如图,正方体ABCD-A1B1C1D1的棱长为2.
如图,正方体ABCD-A1B1C1D1的棱长为2.(1)求异面直线BC1与B1D1所成的角;
(2)求三棱锥A1-AB1D1的体积.
考点:棱柱、棱锥、棱台的体积,异面直线及其所成的角
专题:空间位置关系与距离
分析:(1)连结BD,DC1,由BD∥B1D1,得∠DBC1是异面直线BC1与B1D1所成的角,由此能求出异面直线BC1与B1D1所成的角.
(2)由VA1-AB1D1=VA-A1B1D1,利用等积法能求出三棱锥A1-AB1D1的体积.
(2)由VA1-AB1D1=VA-A1B1D1,利用等积法能求出三棱锥A1-AB1D1的体积.
解答:
解:(1)连结BD,DC1,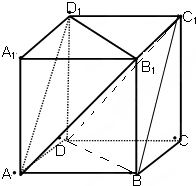
∵BD∥B1D1,∴∠DBC1是异面直线BC1与B1D1所成的角,
∵BD=BC1=DC1,
∴∠DBC1=60°,
∴异面直线BC1与B1D1所成的角为60°.
(2)∵AA1⊥平面A1B1D1,且AA1=2,
S△A1B1D2=
×2×2=2,
∴VA1-AB1D1=VA-A1B1D1
=
×S△A1B1D1×AA1=
×2×2=
.

∵BD∥B1D1,∴∠DBC1是异面直线BC1与B1D1所成的角,
∵BD=BC1=DC1,
∴∠DBC1=60°,
∴异面直线BC1与B1D1所成的角为60°.
(2)∵AA1⊥平面A1B1D1,且AA1=2,
S△A1B1D2=
| 1 |
| 2 |
∴VA1-AB1D1=VA-A1B1D1
=
| 1 |
| 3 |
| 1 |
| 3 |
| 4 |
| 3 |
点评:本题考查异面直线所成角的大小的求法,考查三棱锥的体积的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
相关题目
已知圆x2+y2+mx-
=0与抛物线y2=4x的准线相切,则m=( )
| 1 |
| 4 |
| A、1 | ||
B、
| ||
C、
| ||
D、
|
 如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为DD1的中点
如图,在棱长为2的正方体ABCD-A1B1C1D1中,E为DD1的中点