题目内容
 已知函数y=f(x),x∈[-1,1]的图象是由以原点为圆心的两段圆弧及原点构成(如图所示),则不等式的f(-x)>f(x)+2
已知函数y=f(x),x∈[-1,1]的图象是由以原点为圆心的两段圆弧及原点构成(如图所示),则不等式的f(-x)>f(x)+2| 3 |
考点:函数奇偶性的性质
专题:函数的性质及应用
分析:根据图象得知是奇函数,从而将“不等式f(-x)>f(x)+2
x”转化为“f(x)<-
x”,再令y=f(x),y=-
x,利用图象求解.
| 3 |
| 3 |
| 3 |
解答:
解:由图象可知,函数是奇函数,
∴不等式f(-x)>f(x)+2
x可转化为:f(x)<-
x,
令y=f(x),y=-
x,如图所示:相交于点A、B两点,
由
得,x=±
,
∴不等式f(x)<-
x的解集为:[-1,-
)∪(0,
),
即不等式的f(-x)>f(x)+2
x的解集是[-1,-
)∪(0,
),
故答案为:[-1,-
)∪(0,
).

∴不等式f(-x)>f(x)+2
| 3 |
| 3 |
令y=f(x),y=-
| 3 |
由
|
| 1 |
| 2 |
∴不等式f(x)<-
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
即不等式的f(-x)>f(x)+2
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:[-1,-
| 1 |
| 2 |
| 1 |
| 2 |
点评:本题考查利用函数图象的相对位置关系来解不等式,奇偶函数图象特征,其中转化为对应的函数,能画其图象是解题的关键.

练习册系列答案
相关题目
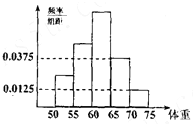 为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为
为了了解某市今年准备报考体育专业的学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1:2:3,则第2小组的频率为 如图阴影部分是圆O的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约
如图阴影部分是圆O的内接正方形,随机撒314粒黄豆,则预测黄豆落在正方形内的约