题目内容
设函数f(x)＝
.
(1)当a＝－5时，求函数f(x)的定义域；
(2)若函数f(x)的定义域为R，求a的取值范围．
解析：(1)当a＝－5时，要使函数f(x)＝有意义，
则|x＋1|＋|x－2|－5≥0.
①当x≤－1时，原不等式可化为－x－1－x＋2－5≥0，即x≤－2；
②当－1＜x≤2时，原不等式可化为x＋1－x＋2≥5，即3≥5，显然不成立；
③当x＞2时，原不等式可化为x＋1＋x－2≥5，即x≥3.
综上所述，所求函数的定义域为(－∞，－2]∪[3，＋∞)．
(2)函数f(x)的定义域为R，则|x＋1|＋|x－2|＋a≥0恒成立，即|x＋1|＋|x－2|≥－a恒成立，
构造h(x)＝|x＋1|＋|x－2|＝
求得函数的最小值为3，
所以a≥－3.故a的取值范围是[－3，＋∞)．
练习册系列答案
教材全解字词句篇系列答案
相关题目
的图象上各点的横坐标伸长到原来的3倍，再向右平移
个单位，得到的函数的一个对称中心是( )
.
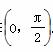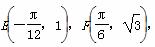求函数f(x)的解析式；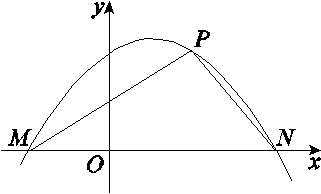
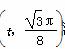满足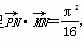
，求函数f(x)的最大值．
＋i的共轭复数为________．
(i是虚数单位)，则|z|＝________．
，
(xy≠0)，则4x＋y的最小值是________．