题目内容
设函数f(x)＝1－|2x－3|.
(1)求不等式f(x)≥3x＋1的解集；
(2)若不等式f(x)－mx≥0的解集非空，求m的取值范围．
解析：(1)由f(x)≥3x＋1，得|2x－3|＋3x≤0，则
即
解得x≤－3，
所以不等式的解集为{x|x≤－3}．
(2)由f(x)＝1－|2x－3|＝
作出f(x)与y＝mx的图象如图所示．
由单调性可知f(x)的最大值点为A
，
又过原点的直线y＝mx过点A时m＝
，与AC平行时m＝2.
故＜m≤2时，y＝f(x)与y＝mx的图象无交点，
故不等式f(x)－mx≥0的解集非空时，m的取值范围是
∪(2，＋∞)．
练习册系列答案
相关题目
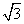sin x,1)，b＝(y，cos x)，且a∥b.
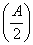＝M，且a＝2，求bc的最大值．
.
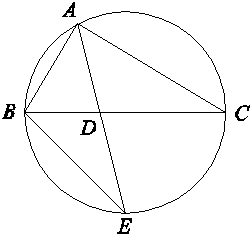
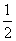AD·AE，求∠BAC的大小．
＋(m2－5m－6)i(m∈R)，试求实数m分别取什么值时，z分别为：
B. 
D．8π