题目内容
如图为一个四棱锥的正视图、侧(左)视图和俯视图,则该四棱锥的表面积为( )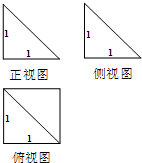

| A、3 | ||
B、2+
| ||
| C、2 | ||
D、3+2
|
考点:由三视图求面积、体积
专题:计算题,空间位置关系与距离
分析:利用三视图画出几何体的图形,通过三视图的数据,求出棱锥的表面积.
解答:
解:由题意可知,四棱锥的底面是边长为1的正方形,其面积S=1×1=1,高h=1,
∴S=1+2×
×1×1+2×
×1×
=2+
.
故选:B.
∴S=1+2×
| 1 |
| 2 |
| 1 |
| 2 |
| 2 |
| 2 |
故选:B.
点评:本题考查三视图与几何体的对应关系,几何体的表面积的求法,考查空间想象能力,计算能力.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线C1:
-
=1(a>0,b>0)与抛物线C2:y2=2px(p>0)有相同焦点,若双曲线C1与抛物线C2的一个公共点为P,且点P到抛物线的准线的距离为p,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、2+
|
设f(n)=2+24+27+210+…+23n+10(n∈N),则f(n)等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
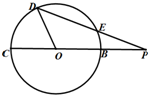 如图,割线PBC经过圆心O,OB=PB=1,又PED交圆O于E,D,且DE=
如图,割线PBC经过圆心O,OB=PB=1,又PED交圆O于E,D,且DE=