题目内容
已知双曲线C1:
-
=1(a>0,b>0)与抛物线C2:y2=2px(p>0)有相同焦点,若双曲线C1与抛物线C2的一个公共点为P,且点P到抛物线的准线的距离为p,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
A、
| ||
B、
| ||
| C、2 | ||
D、2+
|
考点:抛物线的简单性质,双曲线的简单性质
专题:计算题,圆锥曲线的定义、性质与方程
分析:由题意,可得P(
,p),p=2c,P代入C1:
-
=1(a>0,b>0),即可求出双曲线的离心率.
| p |
| 2 |
| x2 |
| a2 |
| y2 |
| b2 |
解答:
解:由题意,可得P(
,p),p=2c
P代入C1:
-
=1(a>0,b>0)可得
-
=1,
∴
-
=1,
∴e=
=
+1.
故选:A.
| p |
| 2 |
P代入C1:
| x2 |
| a2 |
| y2 |
| b2 |
| p2 |
| 4a2 |
| p2 |
| b2 |
∴
| 4c2 |
| 4a2 |
| 4c2 |
| c2-a2 |
∴e=
| c |
| a |
| 2 |
故选:A.
点评:本题考查双曲线的离心率的求法,解题时要熟练掌握双曲线和抛物线的简单性质,是中档题.

练习册系列答案
相关题目
已知某个几何体的三视图如图,根据图中标出的尺寸,可得这个几何体的表面积是( )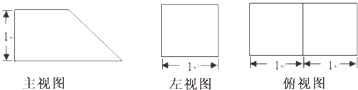

A、
| ||
B、7+
| ||
C、7+2
| ||
D、10+
|
如图为一个四棱锥的正视图、侧(左)视图和俯视图,则该四棱锥的表面积为( )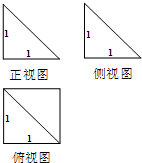

| A、3 | ||
B、2+
| ||
| C、2 | ||
D、3+2
|
“a≤0”是“函数f(x)=|(ax-1)x|在区间(0,+∞)内单调递增”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |