题目内容

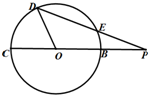如图，割线PBC经过圆心O，OB=PB=1，又PED交圆O于E，D，且DE=
4
7
7
，则△OPD的面积为
 
．
考点：正弦定理
专题：计算题,解三角形
分析：在△ODE中，由余弦定理先求出cos∠EDO=
2
7
7
，在△POD中即有cos∠EDO=
PD2+OD2-OP2
2×DO×PD
=
PD2+1-22
2PD
=
2
7
7
，从而可求出PD，故由海伦公式可求△OPD的面积．
解答： 解：已知，OE=OD=OB=1，DE=
4
7
7
，在△ODE中，由余弦定理知，cos∠EDO=
DO2+DE2-OE2
2×DO×DE
=
2
7
7

OB=PB=1，OP=2
在△POD中，有cos∠EDO=
PD2+OD2-OP2
2×DO×PD
=
PD2+1-22
2PD
=
2
7
7

上式可化为PD2-
4
7
7
PD-3=0，解得PD=
7
或者-
3
7
7
（舍去），
在△POD中，由海伦公式得P=
OD+OP+DP
2
=
3+
7
2

S△OPD=
p(p-OD)(p-OP)(p-PD)
=
3+
7
2
×
1+
7
2
×
7
-1
2
×
3-
7
2
=
3
4
=
3
2

故答案为：
3
2
．
点评：本题考察了余弦定理，海伦公式的综合应用，考察计算能力，属于中档题．
练习册系列答案
相关题目
下列哪一组函数相等（　　）
A、f（x）=x与g（x）=
x2
x
B、f(x)=x2与g(x)=(
x
)4
C、f(x)=|x|与g(x)=(
x
)2
D、f（x）=x2与g（x）=
3x6
已知函数f（x）=
ex
a
-
a
ex
，（a∈R且a＞0）．
（1）判断函数f（x）的单调性，并证明；
（2）若函数f（x）的定义域为（-2，2）时，求使f（1-m）-f（m2-1）＜0成立的实数m的取值范围．
已知函数f1（x）=lg（-x-1）的定义域为M，函数f2（x）=lg（x-3）的定义域为N，A=N∪M，函数g（x）=2x-a（x≤2）的值域为B．
（1）求A、B；
（2）若函数A∩B=B，求实数a的取值范围．
函数f（x）=2x+log2x-3在区间（1，2）内的零点个数是（　　）
A、0B、1C、2D、3
设F1，F2分别是椭圆
x2
a2
+
y2
b2
=1（a＞b＞0）的左、右焦点，若椭圆上存在点A，使∠F1AF2=90°且|AF1|=3|AF2|，则椭圆的离心率为
 
．
已知f（x）是定义在R上的奇函数，且对任意实数x∈R均有f（x-1）=f（x+1），当x∈[0，1）时，f（x）=2x-1，则f（log
1
2
6）=
 
．
如图为一个四棱锥的正视图、侧（左）视图和俯视图，则该四棱锥的表面积为（　　）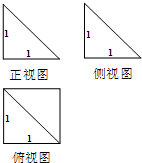
A、3
B、2+
2
C、2
D、3+2
2
函数f（x）=-x2-4x+1（-3≤x≤3）的值域是（　　）
A、（-4，5]
B、[-20，4]
C、[-20，5]
D、[4，5]

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网