题目内容
14.设a=sin$\frac{π}{5}$,b=log${\;}_{\sqrt{2}}$$\sqrt{3}$,c=($\frac{1}{4}$)${\;}^{\frac{2}{3}}$,则( )| A. | a<c<b | B. | b<a<c | C. | c<a<b | D. | c<b<a |
分析 利用三角函数、对数函数、指数函数的单调性直接求解.
解答 解:∵$\frac{1}{2}$=sin$\frac{π}{6}$<a=sin$\frac{π}{5}$<1,
b=log${\;}_{\sqrt{2}}$$\sqrt{3}$>$lo{g}_{\sqrt{2}}\sqrt{2}$=1,
c=($\frac{1}{4}$)${\;}^{\frac{2}{3}}$=($\frac{1}{2}$)${\;}^{\frac{4}{3}}$<$\frac{1}{2}$,
∴c<a<b.
故选:C.
点评 本题考查三个数的大小的求法,是基础题,解题时要认真审题,注意函数性质的合理运用.

练习册系列答案
 互动英语系列答案
互动英语系列答案
相关题目
5.若实数x,y满足不等式组$\left\{\begin{array}{l}{y-x≥0}\\{x+y-7≤0}\\{x≥0}\end{array}\right.$,则z=2x+y的最大值是( )
| A. | $\frac{7}{2}$ | B. | $\frac{21}{2}$ | C. | 14 | D. | 21 |
19.已知a>2,b>2,直线$y=-\frac{b}{a}x+b$与曲线(x-1)2+(y-1)2=1只有一个公共点,则ab的取值范围为( )
| A. | $(4,6+4\sqrt{2})$ | B. | $(4,6+4\sqrt{2}]$ | C. | $[6+4\sqrt{2},+∞)$ | D. | $(6+4\sqrt{2},+∞)$ |
4.已知集合A={x|x2-2x-3<0},集合B={x|2x-1≥1},则A∩B=( )
| A. | [-1,3) | B. | [0,3) | C. | [1,3) | D. | (1,3) |
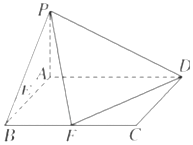 已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.
已知在四棱锥P-ABCD中,底面ABCD是矩形,且AD=2,AB=1,PA⊥平面ABCD,E,F分别是线段AB,BC的中点.