题目内容
已知等差数列{an}的项数为2n，若a1+a3+…+a2n-1=72，a2+a4+…+a2n=90，且a2n-a1=33，求数列的公差d．
考点：等差数列的性质
专题：计算题,等差数列与等比数列
分析：先由等差数列的性质将a1+a3+…+a2n-1=72，a2+a4+…+a2n=90，转化为n，d的关系，再将a2n-a1=33转化为n，d的关系，建立方程求解．
解答：
解：∵a1+a3+…+a2n-1=72，（1）
a2+a4+…+a2n=90，（2）
（2）-（1）得nd=18①
a2n-a1=（2n-1）d=33②
由①②得d=3．
a2+a4+…+a2n=90，（2）
（2）-（1）得nd=18①
a2n-a1=（2n-1）d=33②
由①②得d=3．
点评：本题主要考查等差数列的性质和通项公式，考查学生的计算能力，比较基础．
练习册系列答案
相关题目
已知函数f（x）=lg（x-1），那么f（x）的定义域是（ ）
| A、R |
| B、{x|x＞1} |
| C、{x|x≠1} |
| D、{x|x≠0} |
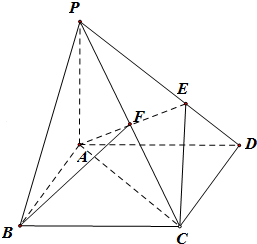如图，在四棱锥P-ABCD中，底面ABCD是菱形，∠ABC=60°，PA⊥平面ABCD，AP=AB=2，E在PD上，且PE=2ED，F是PC的中点，
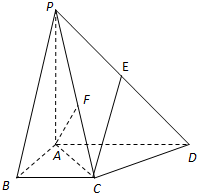如图，在四棱锥P-ABCD中，平面PAC⊥平面ABCD，且PA⊥AC，PA=AD=2AB=2BC．BC∥AD，AB⊥AD．已知数列{an}的前n项和为Sn，且Sn=2an-1（n∈N*），则a4=（ ）
| A、8 | B、16 | C、31 | D、32 |
设是虚数单位，若复数
为实数，则实数a的值为（ ）
| a-i |
| 2+i |
| A、-2 | ||
| B、2 | ||
C、-
| ||
D、
|