题目内容
已知集合A={x|log2(6x+12)≥log2(x2+3x+2),x∈R},B={x|2 x2-m<4x,x∈R}
(1)当m=3时,求A∩(∁RB).
(2)若A∩B={x|-1<x<4},求实数m的值.
(1)当m=3时,求A∩(∁RB).
(2)若A∩B={x|-1<x<4},求实数m的值.
考点:交集及其运算,交、并、补集的混合运算
专题:函数的性质及应用,集合
分析:(1)由对数函数、指数函数的性质求出集合A和B,由补集和交集的运算求出A∩(∁RB);
(2)由指数函数的性质化简2 x2-m<4x,再由A∩B={x|-1<x<4},求出实数m的值.
(2)由指数函数的性质化简2 x2-m<4x,再由A∩B={x|-1<x<4},求出实数m的值.
解答:
解:(1)由log2(6x+12)≥log2(x2+3x+2)得,
,解得-1≤x≤5,即A={x|-1<x≤5},
因为m=3,且2 x2-m<4x=22x,所以x2-3<2x,
解得-1<x<3,即B={x|-1<x<3},
所以CRB={x|x≤-1或x≥3}.
则A∩CRB={x|3≤x≤5},
(2)由2 x2-m<4x=22x得,x2-m<2x,即x2-2x-m<0,
因为A∩B={x|-1<x<4},且A={x|-1<x≤5},
所以4是方程x2-2x-m=0的一个根,代入得m=8,
则实数m的值是8.
|
因为m=3,且2 x2-m<4x=22x,所以x2-3<2x,
解得-1<x<3,即B={x|-1<x<3},
所以CRB={x|x≤-1或x≥3}.
则A∩CRB={x|3≤x≤5},
(2)由2 x2-m<4x=22x得,x2-m<2x,即x2-2x-m<0,
因为A∩B={x|-1<x<4},且A={x|-1<x≤5},
所以4是方程x2-2x-m=0的一个根,代入得m=8,
则实数m的值是8.
点评:本题考查集合的交、并、补集的混合运算,以及对数函数、指数函数的性质,属于中档题.

练习册系列答案
 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案 轻松课堂单元测试AB卷系列答案
轻松课堂单元测试AB卷系列答案
相关题目
关于直线m,n与平面α,β,γ有以下三个命题,其中真命题有( )
(1)若m∥α,n∥β,且α∥β则m∥n
(2)若α∩β=m,α⊥γ,β⊥γ则m⊥γ(3)若m⊥α,n⊥β且α⊥β则m⊥n.
(1)若m∥α,n∥β,且α∥β则m∥n
(2)若α∩β=m,α⊥γ,β⊥γ则m⊥γ(3)若m⊥α,n⊥β且α⊥β则m⊥n.
| A、1个 | B、2个 | C、3个 | D、0个 |
在同一坐标系中,函数y=3x的图与y=(
)x的图象( )
| 1 |
| 3 |
| A、关于x轴对称 |
| B、关于y轴对称 |
| C、关于原点对称 |
| D、关于直线y=x对称 |
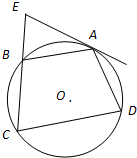 如图,四边形ABCD的外接圆为⊙O,EA是⊙O的切线,CB的延长线与EA相交于点E,AB=AD.求证:AB2=BE•CD.
如图,四边形ABCD的外接圆为⊙O,EA是⊙O的切线,CB的延长线与EA相交于点E,AB=AD.求证:AB2=BE•CD.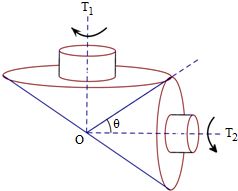 如图所示,某传动装置由两个陀螺T1,T2组成,陀螺之间没有滑动.每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的
如图所示,某传动装置由两个陀螺T1,T2组成,陀螺之间没有滑动.每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成,每个圆柱的底面半径和高都是相应圆锥底面半径的