题目内容
点P为抛物线y2=2x上的任意一点，求点P到直线x-2y+4=0的最短距离．
考点：抛物线的简单性质
专题：圆锥曲线的定义、性质与方程
分析：根据过P点作直线x-2y+4=0平行线，与抛物线y2=2x相切，
可以判断此时P点到直线的 距离最近，与用导数求解得出P（2，2），再运用点到直线的距离即可．
可以判断此时P点到直线的 距离最近，与用导数求解得出P（2，2），再运用点到直线的距离即可．
解答：
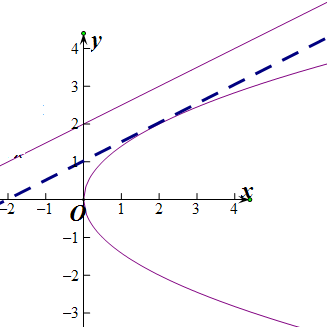解：过P点作直线x-2y+4=0平行线，与抛物线y2=2x相切，
可以判断此时P点到直线的 距离最近，
P（x0，y0），
∵y2=2x，
∴y＞0时，y=
，y′=
，
∴
=
，x0=2，y0=2，
即P（2，2）
d=
=
，
故点P到直线x-2y+4=0的最短距离
．
解：过P点作直线x-2y+4=0平行线，与抛物线y2=2x相切，可以判断此时P点到直线的 距离最近，
P（x0，y0），
∵y2=2x，
∴y＞0时，y=
| 2x |
| 1 | ||
|
∴
| 1 | ||
|
| 1 |
| 2 |
即P（2，2）
d=
| |2-2×2+4| | ||
|
2
| ||
| 5 |
故点P到直线x-2y+4=0的最短距离
2
| ||
| 5 |
点评：本题考查了直线与曲线的位置关系，借助导数判断最值即可，关键求解导数确定点的坐标，难度不大，有点综合．
练习册系列答案
相关题目
已知椭圆关于直线m，n与平面α，β，γ有以下三个命题，其中真命题有（ ）
（1）若m∥α，n∥β，且α∥β则m∥n
（2）若α∩β=m，α⊥γ，β⊥γ则m⊥γ（3）若m⊥α，n⊥β且α⊥β则m⊥n．
（1）若m∥α，n∥β，且α∥β则m∥n
（2）若α∩β=m，α⊥γ，β⊥γ则m⊥γ（3）若m⊥α，n⊥β且α⊥β则m⊥n．
| A、1个 | B、2个 | C、3个 | D、0个 |
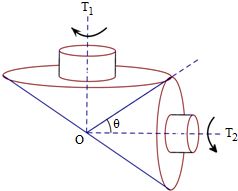如图所示，某传动装置由两个陀螺T1，T2组成，陀螺之间没有滑动．每个陀螺都由具有公共轴的圆锥和圆柱两个部分构成，每个圆柱的底面半径和高都是相应圆锥底面半径的执行如图所示的程序框图，则输出n的值是（ ）
| A、8 | B、9 | C、10 | D、11 |