题目内容
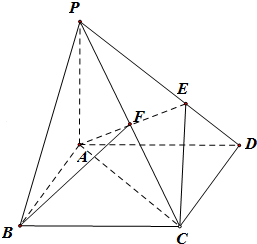 如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中点,
如图,在四棱锥P-ABCD中,底面ABCD是菱形,∠ABC=60°,PA⊥平面ABCD,AP=AB=2,E在PD上,且PE=2ED,F是PC的中点,(1)证明:平面PBD⊥平面PAC;
(2)求证:BF∥平面ACE;
(3)求三棱锥D-BCF的体积V.
考点:棱柱、棱锥、棱台的体积,直线与平面平行的判定,平面与平面垂直的判定
专题:空间位置关系与距离
分析:(Ⅰ)连接BD,交AC于O,由已知得AC⊥BD,PA⊥BD,BD⊥面PAC,由此能证明平面PBD⊥平面PAC.
(Ⅱ)取PE的中点G,连BG,FG,由已知得BG∥OE,EG∥CE,从而平面BFG∥平面ACE,由此能证明BF∥平面ACE.
(Ⅲ)由VD-BCF=VF-BCD,利用等积法能求出三棱锥D-BCF的体积.
(Ⅱ)取PE的中点G,连BG,FG,由已知得BG∥OE,EG∥CE,从而平面BFG∥平面ACE,由此能证明BF∥平面ACE.
(Ⅲ)由VD-BCF=VF-BCD,利用等积法能求出三棱锥D-BCF的体积.
解答:
(Ⅰ)证明:连接BD,交AC于O,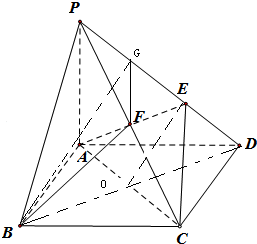
因为底面ABCD是菱形,所以AC⊥BD,又PA⊥平面ABCD,
所以PA⊥BD,BD⊥面PAC,
故平面PBD⊥平面PAC.
(Ⅱ)证明:取PE的中点G,连BG,FG,
由F是PC的中点,O是BD的中点,得
BG∥OE,EG∥CE,所以平面BFG∥平面ACE,
故BF∥平面ACE.
(Ⅲ)解:VD-BCF=VF-BCD
=
×S△BCD×
AP
=
×
×2×2×sin120°×
×2
=
.

因为底面ABCD是菱形,所以AC⊥BD,又PA⊥平面ABCD,
所以PA⊥BD,BD⊥面PAC,
故平面PBD⊥平面PAC.
(Ⅱ)证明:取PE的中点G,连BG,FG,
由F是PC的中点,O是BD的中点,得
BG∥OE,EG∥CE,所以平面BFG∥平面ACE,
故BF∥平面ACE.
(Ⅲ)解:VD-BCF=VF-BCD
=
| 1 |
| 3 |
| 1 |
| 2 |
=
| 1 |
| 3 |
| 1 |
| 2 |
| 1 |
| 2 |
=
| ||
| 3 |
点评:本小题主要考查空间线面关系、几何体的体积等知识,考查数形结合、化归与转化的数学思想方法,以及空间想象能力、推理论证能力和运算求解能力.

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
若2x=8Y+1且9y=3x-9,则x+y的值是( )
| A、18 | B、24 | C、21 | D、27 |
已知实数x,y满足
,则点(x,y)在函数f(x)=
的图象与坐标轴所围成的封闭图形的内部的概率为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
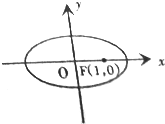 已知椭圆
已知椭圆