题目内容
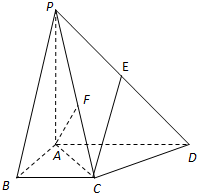 如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.
如图,在四棱锥P-ABCD中,平面PAC⊥平面ABCD,且PA⊥AC,PA=AD=2AB=2BC.BC∥AD,AB⊥AD.(1)若点E为PD的中点,求证:CE∥平面PAB;
(2)在平面PAC内,AF⊥PC.求证:AF⊥平面PCD.
考点:直线与平面垂直的判定,直线与平面平行的判定
专题:空间位置关系与距离
分析:(1)取PA的中点为G,连接BG、EG,得到四边形BGEC为平行四边形,所以EC∥BG;
(2)因为AB⊥AD,BC∥AD,AB=BC,AD=2BC,易证得CD⊥AC.判断CD⊥平面PAC,得到CD⊥AF结合已知和线面平行的判定定理解得.
(2)因为AB⊥AD,BC∥AD,AB=BC,AD=2BC,易证得CD⊥AC.判断CD⊥平面PAC,得到CD⊥AF结合已知和线面平行的判定定理解得.
解答:

证明:(1)取PA的中点为G,连接BG、EG,则EG∥
AD,EG=
AD,------------(1分)
又BC∥AD,BC=
AD,所以EG∥BC,EG=BC,四边形BGEC为平行四边形.-------------(2分)
所以EC∥BG.----------------------------------------(3分)
又EC?平面PAB,BG?平面PAB,
故EC∥平面PAB.----------------------------------------(5分)
(2)因为AB⊥AD,BC∥AD,AB=BC,AD=2BC,易证得CD⊥AC.-----------------------(8分)
因为PA⊥平面ABCD,所以PA⊥CD,
因为PA∩AC=A,所以CD⊥平面PAC.----(10分)
而AF?平面PAC,所以CD⊥AF.又已知AF⊥PC
又因为CD∩PC=C,所以AF⊥平面PCD.(12分)

证明:(1)取PA的中点为G,连接BG、EG,则EG∥
| 1 |
| 2 |
| 1 |
| 2 |
又BC∥AD,BC=
| 1 |
| 2 |
所以EC∥BG.----------------------------------------(3分)
又EC?平面PAB,BG?平面PAB,
故EC∥平面PAB.----------------------------------------(5分)
(2)因为AB⊥AD,BC∥AD,AB=BC,AD=2BC,易证得CD⊥AC.-----------------------(8分)
因为PA⊥平面ABCD,所以PA⊥CD,
因为PA∩AC=A,所以CD⊥平面PAC.----(10分)
而AF?平面PAC,所以CD⊥AF.又已知AF⊥PC
又因为CD∩PC=C,所以AF⊥平面PCD.(12分)
点评:本题考查了线面平行的判定定理以及线面垂直的判定定理的运用关键是熟练定理和性质的运用.

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
已知实数x,y满足
,则点(x,y)在函数f(x)=
的图象与坐标轴所围成的封闭图形的内部的概率为( )
|
|
A、
| ||
B、
| ||
C、
| ||
D、
|
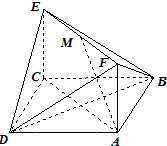 如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=
如图,已知正方形ABCD和矩形ACEF所在平面互相垂直,AB=