题目内容
若对定义在R上的可导函数f（x）恒有（4-x）f（x）+xf′（x）＞0，则f（x）（ ）
| A、恒大于等于0 |
| B、恒小于0 |
| C、恒大于0 |
| D、和0的大小关系不能确定 |
考点：导数的运算
专题：导数的概念及应用
分析：根据条件构造函数g（x）=
，利用导数研究函数g（x）的单调性和极值，进而可以判断函数f（x）的取值情况．
| x4f(x) |
| ex |
解答：
解：令g（x）=
，
∴g′（x）=
∵（4-x）f（x）+xf′（x）＞0恒成立，
∴当x＞0时，g'（x）＞0，此时函数g（x）单调递增，
当x＜0时，g'（x）＜0，此时函数g（x）单调递减，
∴当x=0时，g（x）取得极小值，同时也是最小值g（0）=0，
∴g（x）=
≥g（0），
即g（x）=
，
当x≠0时，g（x）＞0，
∴当x≠0时，f（x）＞0，
∵（4-x）f（x）+xf′（x）＞0恒成立，
∴当x=0时，4f（0）+0＞0恒成立，
∴f（0）＞0，
综上无论x取何值，恒有f（x）＞0，
故选：C．
| x4f(x) |
| ex |
∴g′（x）=
| x3[(x-4)f(x)+xf′(x)] |
| ex |
∵（4-x）f（x）+xf′（x）＞0恒成立，
∴当x＞0时，g'（x）＞0，此时函数g（x）单调递增，
当x＜0时，g'（x）＜0，此时函数g（x）单调递减，
∴当x=0时，g（x）取得极小值，同时也是最小值g（0）=0，
∴g（x）=
| x4f(x) |
| ex |
即g（x）=
| x4f(x) |
| ex |
当x≠0时，g（x）＞0，
∴当x≠0时，f（x）＞0，
∵（4-x）f（x）+xf′（x）＞0恒成立，
∴当x=0时，4f（0）+0＞0恒成立，
∴f（0）＞0，
综上无论x取何值，恒有f（x）＞0，
故选：C．
点评：本题主要考查函数值判断，利用条件构造函数g（x）=
是解决本题的关键，利用导数研究函数的单调性和极值，考查学生的观察能力，综合性较强，难度较大．
| x4f(x) |
| ex |
练习册系列答案
目标测试系列答案
相关题目
设正弦函数f（x）=cosx在x=0和x=
处得切线得斜率分别为k1，k2，则k1，k2的大小关系为（ ）
| π |
| 2 |
| A、k1＜k2 |
| B、k1＞k2 |
| C、k1=k2 |
| D、不确定 |
抛物线x2=4y的焦点到双曲线y2-
=1的渐近线的距离等于（ ）
| x2 |
| 4 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
若3a，b，c成等比数列，则函数f（x）=ax3+bx2+cx+d的零点个数为（ ）
| A、0 | B、1 | C、2 | D、3 |
如图是某空间几何体的直观图，则该几何体的侧视图是（ ）
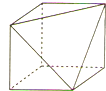
A、 |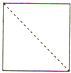
B、 |
C、 |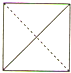
D、 |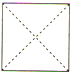
近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征召n名义务宣传志愿者，成立环境保护宣传组织．现把该组织的成员按年龄分成5组：第1组[20，25），第2组[25，30），第3组[30，35），第4组[35，40），第5组[40，45]，得到的频率分布直方图如图所示，已知第2组有35人．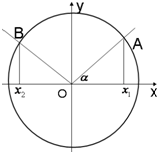
已知角α的始边与x轴的非负半轴重合，终边与单位圆O交于点A（x1，y1），将射线OA按逆时针方向旋转