题目内容
设x0是函数f（x）=lnx+x-4的零点，则x0所在的区间为（ ）
| A、（0，1） |
| B、（1，2） |
| C、（2，3） |
| D、（3，4） |
考点：函数零点的判定定理
专题：函数的性质及应用
分析：由函数的解析式可得 f（2）＜0，f（3）＞0，再根据函数的零点的判定定理求得函数的零点x0所在的区间．
解答：
解：∵x0是函数f（x）=1nx+x-4的零点，f（2）=ln2-2＜0，f（3）=ln3-1＞0，
∴函数的零点x0所在的区间为（2，3），
故选C．
∴函数的零点x0所在的区间为（2，3），
故选C．
点评：本题主要考查函数的零点的判定定理的应用，属于基础题．
练习册系列答案
口算题天天练系列答案
相关题目
设
，
是两个非零向量，则下列结论不正确的是（ ）
| a |
| b |
A、|
| ||||||||||||
B、若
| ||||||||||||
C、若存在一个实数k满足
| ||||||||||||
D、若
|
若函数f（x）=2（a-1）x-x2在区间（-∞，4]上是增函数，则实数a的取值范围是（ ）
| A、a≤-3 | B、a≥-3 |
| C、a≤5 | D、a≥5 |
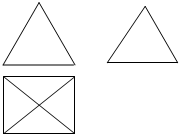如图是一个空间几何体的三视图，如果主视图和左视图都是边长为2的正三角形，俯视图为正方形，那么该几何体的体积为
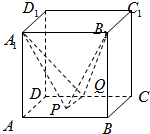如图，设正方体ABCD-A1B1C1D1的棱长为1，P是底面ABCD上的动点，Q是线段DC上的动点，且四面体A1B1PQ的体积为
曲线y=xcosx在x=
处的切线的斜率是（ ）
| π |
| 3 |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|