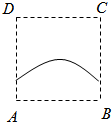题目内容

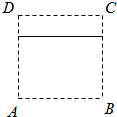
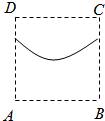
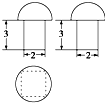已知一个几何体的三视图如图所示，则该几何体的表面积为（　　）
A、24+6π
B、24+4π
C、28+6π
D、28+4π
考点：由三视图求面积、体积
专题：计算题
分析：由三视图可知该几何体上部分为半球，下部分为长方体，然后根据长方体和球的表面积公式求组合体的表面积即可．
解答： 解：由三视图可知该几何体上部分为半球，下部分为长方体，
球的直径为2r=2
2
，即球半径r=
2
．
长方体的底面为正方形边长为2，高为3．
∴该几何体的表面积为
1
2
×4π×(
2
)2+π×(
2
)2+4×2×3=4π+2π+24=24+6π．
故选：A．
点评：本题主要考查三视图的应用，以及空间几何体的表面积求法，要求熟练掌握常见几何体的表面积公式．
练习册系列答案
相关题目
一枚硬币，连掷两次，至少有一次正面朝上的概率为（　　）
A、
1
2
B、
1
3
C、
1
4
D、
3
4
从10个事件中任取一个事件，若这个事件是必然事件的概率为0.2，是不可能事件的概率为0.3，则这10个事件中随机事件的个数是（　　）
A、3B、4C、5D、6
设关于x的方程2x+2-4x-b=0．
（Ⅰ） 如果b=1，求实数x的值；
（Ⅱ） 如果2x≤16且log2x≥0，求实数b的取值范围．
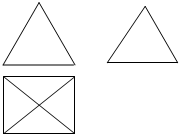如图是一个空间几何体的三视图，如果主视图和左视图都是边长为2的正三角形，俯视图为正方形，那么该几何体的体积为
 
．
已知椭圆G：
x2
4
+y2=1，过点（m，0）作圆x2+y2=1的切线L交椭圆G于A，B两点．
（1）求椭圆G的焦点坐标和离心率；
（2）求m的取值范围；
（3）将|AB|表示为m的函数，并求|AB|的最大值．
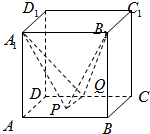如图，设正方体ABCD-A1B1C1D1的棱长为1，P是底面ABCD上的动点，Q是线段DC上的动点，且四面体A1B1PQ的体积为
1
8
，则P的轨迹为（　　）
A、
B、
C、
D、
若实数a、b满足
-π≤a≤π
-π≤b≤π
，则使得f（x）=x2+2ax-b2+π2有零点的概率为（　　）
A、1-
3
4
π
B、1-
π
4
C、1-
π
8
D、1-
π
2
已知函数ft(x)=(x-t)2-t（t∈R），设a＜b，f(x)=
fa(x)，fa(x)＜fb(x)
fb(x)，fa(x)≥fb(x)
，若函数f（x）+x+a-b有四个零点，则b-a的取值范围是（　　）
A、(2+
5
，+∞)
B、(0，2+
5
)
C、(0，2+
3
)
D、(2+
3
，+∞)

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网