题目内容

若a=log
1
3
2，b=20.1，c=(
1
2
)0.3，则下列结论成立的是（　　）
A、a＜b＜c
B、a＜c＜b
C、b＜c＜a
D、b＜a＜c
考点：对数值大小的比较
专题：计算题
分析：通过1或者0做中介判断三个数与1和0的大小即可得到结果．
解答： 解：∵a=log
1
3
2＜0，b=20.1＞1；c=(
1
2
)0.3∈（0，1），
∴a＜c＜b．
故选：B．
点评：本题主要考查指数函数、对数函数的单调性与特殊点的问题．要熟记一些特殊点，比如logaa=1，loga1=0．
练习册系列答案
相关题目
已知a＞0且a≠1，函数f(x)=
ax-1
ax+1

（1）解关于x的不等式f（x）＞0； 
（2）当a=2时，求证：方程f（x）=lnx在区间（1，2）内至少有一个根．
若双曲线x2-y2=1与圆（x-1）2+y2=a2（a＞0）恰有三个不同的公共点，则a=
 
．
设
a
，
b
是两个非零向量，则下列结论不正确的是（　　）
A、|
a
+
b
|＞|
a
-
b
|
B、若
a
=
b
，则|
a
|=|
b
|
C、若存在一个实数k满足
a
=k
b
，则
a
与
b
共线
D、若
a
与
b
为同方向的向量，则|
a
+
b
|=|
a
|+|
b
|
如图是一几何体的三视图，则此几何体的体积是（　　）
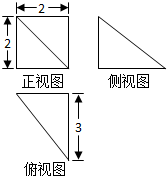
A、4B、8C、12D、4π
一枚硬币，连掷两次，至少有一次正面朝上的概率为（　　）
A、
1
2
B、
1
3
C、
1
4
D、
3
4
已知直线L经过定点A（4，1），在x轴，y轴上的截距分别为a，b，且a，b都大于零，则a+b的最小值为
 
．
若函数f（x）=2（a-1）x-x2在区间（-∞，4]上是增函数，则实数a的取值范围是（　　）
A、a≤-3B、a≥-3
C、a≤5D、a≥5
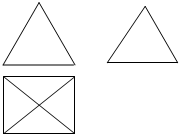如图是一个空间几何体的三视图，如果主视图和左视图都是边长为2的正三角形，俯视图为正方形，那么该几何体的体积为
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网