题目内容
设n为正整数,f(n)=1+
+
+…+
,计算得f(2)=
,f(4)>2,f(8)>
,f(16)>3,观察上述结果,当n≥2时,可推测一般的结论为 .
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| n |
| 3 |
| 2 |
| 5 |
| 2 |
考点:归纳推理
专题:规律型
分析:已知的式子可化为f(21)=
,f(22)>
,f(23)>
,f(24)>
,由此规律可得f(2n)>
.
| 2+1 |
| 2 |
| 2+2 |
| 2 |
| 3+2 |
| 2 |
| 4+2 |
| 2 |
| n+2 |
| 2 |
解答:
解:由题意得f(2)=
可化为f(21)=
,
同理f(4)>2可化为f(22)>
,
f(8)>
可化为f(23)>
,
f(16)>3可化为f(24)>
,
以此类推,可得f(2n)>
,
故答案为:f(2n)>
| 3 |
| 2 |
| 2+1 |
| 2 |
同理f(4)>2可化为f(22)>
| 2+2 |
| 2 |
f(8)>
| 5 |
| 2 |
| 3+2 |
| 2 |
f(16)>3可化为f(24)>
| 4+2 |
| 2 |
以此类推,可得f(2n)>
| n+2 |
| 2 |
故答案为:f(2n)>
| n+2 |
| 2 |
点评:本题考查归纳推理,把已知的式子变形找规律是解决问题的关键,属基础题.

练习册系列答案
 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案
相关题目
若函数f(x)=2(a-1)x-x2在区间(-∞,4]上是增函数,则实数a的取值范围是( )
| A、a≤-3 | B、a≥-3 |
| C、a≤5 | D、a≥5 |
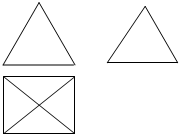 如图是一个空间几何体的三视图,如果主视图和左视图都是边长为2的正三角形,俯视图为正方形,那么该几何体的体积为
如图是一个空间几何体的三视图,如果主视图和左视图都是边长为2的正三角形,俯视图为正方形,那么该几何体的体积为 如图,满足条件
如图,满足条件