题目内容
已知函数y=x+
有如下性质:如果常数a>0,那么该函数在(0,
]上是减函数,在[
,+∞)上是增函数.
(Ⅰ)若函数y=x+
(x>0)的值域为[6,+∞),求实数b的值;
(Ⅱ)已知f(x)=
,x∈[0,1],求函数f(x)的单调区间和值域;
(Ⅲ)对于(Ⅱ)中的函数f(x)和函数g(x)=-x-2c,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数c的值.
| a |
| x |
| a |
| a |
(Ⅰ)若函数y=x+
| 2b |
| x |
(Ⅱ)已知f(x)=
| 4x2-12x-3 |
| 2x+1 |
(Ⅲ)对于(Ⅱ)中的函数f(x)和函数g(x)=-x-2c,若对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,求实数c的值.
考点:函数最值的应用,函数的值域,函数单调性的判断与证明
专题:函数的性质及应用
分析:(Ⅰ)由所给函数y=x+
(x>0)性质知,即可得出对于函数y=x+
,当x=
时取得最小值2
,可得2
=6,解出即可.
(II)设t=2x+1,t∈[1,3],f(t)=
=t+
-8(t∈[1,3]).由所给函数y=x+
(x>0)性质知:f(t)在[1,2]单调递减,[2,3]单调递增.进而取得最值.
(III)g(x)在[0,1]单调递减,可得g(x)∈[-1-2c,-2c].对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,?[-4,-3]⊆[-1-2c,-2c],解出即可.
| a |
| x |
| 2b |
| x |
| 2b |
| 2b |
| 2b |
(II)设t=2x+1,t∈[1,3],f(t)=
| t2-8t+4 |
| t |
| 4 |
| t |
| a |
| x |
(III)g(x)在[0,1]单调递减,可得g(x)∈[-1-2c,-2c].对任意x1∈[0,1],总存在x2∈[0,1],使得g(x2)=f(x1)成立,?[-4,-3]⊆[-1-2c,-2c],解出即可.
解答:
解:(Ⅰ)由所给函数y=x+
(x>0)性质知,当x>0时,x=
时函数取最小值2
;
∴对于函数y=x+
,当x=
时取得最小值2
,
∴2
=6,
解得b=log29=2log23.
(Ⅱ)设t=2x+1,t∈[1,3],f(t)=
=t+
-8(t∈[1,3]),
由所给函数y=x+
(x>0)性质知:f(t)在[1,2]单调递减,[2,3]单调递增.
∴f(x)在[0,
]单调递减,在[
,1]单调递增.
于是f(x)min=f(
)=-4,f(x)max=max{f(0),f(1)}=-3,
∴f(x)∈[-4,-3].
(Ⅲ)∵g(x)在[0,1]单调递减,∴g(x)∈[-1-2c,-2c],
由题意知:[-4,-3]⊆[-1-2c,-2c]
于是有:
,
解得:c=
.
| a |
| x |
| a |
| a |
∴对于函数y=x+
| 2b |
| x |
| 2b |
| 2b |
∴2
| 2b |
解得b=log29=2log23.
(Ⅱ)设t=2x+1,t∈[1,3],f(t)=
| t2-8t+4 |
| t |
| 4 |
| t |
由所给函数y=x+
| a |
| x |
∴f(x)在[0,
| 1 |
| 2 |
| 1 |
| 2 |
于是f(x)min=f(
| 1 |
| 2 |
∴f(x)∈[-4,-3].
(Ⅲ)∵g(x)在[0,1]单调递减,∴g(x)∈[-1-2c,-2c],
由题意知:[-4,-3]⊆[-1-2c,-2c]
于是有:
|
解得:c=
| 3 |
| 2 |
点评:本题考查了“双勾函数”函数y=x+
(x>0)性质及其应用、恒成立问题的等价转化等基础知识与基本技能方法,考查了分析问题和解决问题的能力,属于难题.
| a |
| x |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
曲线y=xcosx在x=
处的切线的斜率是( )
| π |
| 3 |
A、-
| ||||||
B、-
| ||||||
C、
| ||||||
D、
|
已知函数ft(x)=(x-t)2-t(t∈R),设a<b,f(x)=
,若函数f(x)+x+a-b有四个零点,则b-a的取值范围是( )
|
A、(2+
| ||
B、(0,2+
| ||
C、(0,2+
| ||
D、(2+
|
已知sinα+cosα=
,且0≤α<π,那么tanα等于( )
| 1 |
| 5 |
A、-
| ||
B、-
| ||
C、
| ||
D、
|
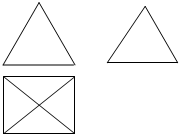 如图是一个空间几何体的三视图,如果主视图和左视图都是边长为2的正三角形,俯视图为正方形,那么该几何体的体积为
如图是一个空间几何体的三视图,如果主视图和左视图都是边长为2的正三角形,俯视图为正方形,那么该几何体的体积为 如图,满足条件
如图,满足条件