题目内容
设F是双曲线
-
=1的焦点,过F作双曲线一条渐近线的垂线,与两条渐近线交于P,Q,若
=3
,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| FQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
考点:双曲线的简单性质
专题:综合题
分析:设F(-c,0),过F作双曲线一条渐近线的垂线方程为y=
(x+c),与两条渐近线方程联立,求出P,Q的横坐标,利用
=3
,建立方程,即可求出双曲线的离心率.
| a |
| b |
| FP |
| FQ |
解答:
解:设F(-c,0),过F作双曲线一条渐近线的垂线方程为y=
(x+c),
与y=-
x联立可得x=-
;与y=
x联立可得x=
,
∵
=3
,
∴
+c=3(-
+c),
∴a2c2=(c2-2a2)(2c2-3a2),
∴e4-4e2+3=0,
∵e>1,
∴e=
.
故选:C.
| a |
| b |
与y=-
| b |
| a |
| a2 |
| c |
| b |
| a |
| a2c |
| b2-a2 |
∵
| FP |
| FQ |
∴
| a2c |
| b2-a2 |
| a2 |
| c |
∴a2c2=(c2-2a2)(2c2-3a2),
∴e4-4e2+3=0,
∵e>1,
∴e=
| 3 |
故选:C.
点评:本题考查双曲线的性质,考查向量知识的运用,确定a,c的关系是关键.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
正三棱柱ABC-A1B1C1的底面边长为2,侧棱长为
,D为BC中点,则三棱锥A-B1DC1的体积为( )
| 3 |
| A、3 | ||||
B、
| ||||
| C、1 | ||||
D、
|
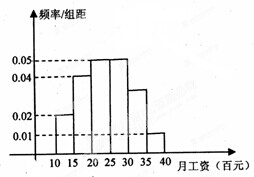 为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )
为了解工薪阶层的收入情况,某地政府调查了1000人的月工资收入,并把调查结果画成如图所示的频率分布直方图,则由图知月工资在(30,35](百元)的人数为( )| A、80 | B、150 |
| C、230 | D、400 |
已知a,b是正数,且a+b=1,则
+
( )
| 1 |
| a |
| 4 |
| b |
| A、有最小值8 |
| B、有最小值9 |
| C、有最大值8 |
| D、有最大值9 |
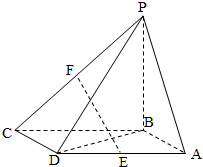 如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD=
如图,四棱锥P-ABCD的底面ABCD是平行四边形,BA=BD= 从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图:
从某校随机抽取100名学生,获得了他们一周课外阅读时间(单位:小时)的数据,整理得到数据分组及频数分布表和频率分布直方图: