题目内容
已知a，b是正数，且a+b=1，则
+
（ ）
| 1 |
| a |
| 4 |
| b |
| A、有最小值8 |
| B、有最小值9 |
| C、有最大值8 |
| D、有最大值9 |
考点：基本不等式
专题：计算题
分析：将式子“
+
”化为（a+b）（
+
），化简后利用基本不等式求出式子的最小值．
| 1 |
| a |
| 4 |
| b |
| 1 |
| a |
| 4 |
| b |
解答：
解：由a+b=1得，
+
=（a+b）（
+
）=5+
+
，
又a、b是正数，
所以
+
≥2
=4，当且仅当
=
时取等号，
则
+
≥5+4=9，
即
+
的最小值为9，
故选B．
| 1 |
| a |
| 4 |
| b |
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 4a |
| b |
又a、b是正数，
所以
| b |
| a |
| 4a |
| b |
|
| b |
| a |
| 4a |
| b |
则
| 1 |
| a |
| 4 |
| b |
即
| 1 |
| a |
| 4 |
| b |
故选B．
点评：本题考查了基本不等式的应用：求最值问题，注意三个条件：一正二定三相等，以及“1”的代换问题．
练习册系列答案
相关题目
将边长为1的正方形以其一边所在直线为旋转轴旋转一周，所得几何体的侧面积是（ ）
| A、4π | B、3π | C、2π | D、π |
设F是双曲线
-
=1的焦点，过F作双曲线一条渐近线的垂线，与两条渐近线交于P，Q，若
=3
，则双曲线的离心率为（ ）
| x2 |
| a2 |
| y2 |
| b2 |
| FP |
| FQ |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
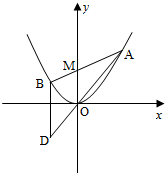如图，已知抛物线C：x2=4y，过点M（0，2）任作一直线与C相交于A，B两点，过点B作y轴的平行线与直线AO相交于点D（O为坐标原点）．