题目内容

18．已知数列{an}的首项a1=1，且an=2an-1+3（n≥2），则an=2n+1-3．

分析 由an=2an-1+3（n≥2），变形为an+3=2（an-1+3），利用等比数列的通项公式即可得出．

解答 解：由an=2an-1+3（n≥2），变形为an+3=2（an-1+3），
∴数列{an+3}是等比数列，首项为4，公比为2．
∴an+3=4×2n-1=2n+1，
∴an=2n+1-3．
故答案为：2n+1-3．

点评 本题考查了递推关系、等比数列的通项公式，考查了变形能力与计算能力，属于中档题．

练习册系列答案
相关题目
8．求平行于直线2x-y+3=0，且与两坐标轴围成的直角三角形的面积为9的直线方程．
9．已知sinαcosα=$\frac{1}{3}$，则sin2α=$\frac{2}{3}$cos4α=$\frac{1}{9}$．
6．若log32=0.6309，则log312=2.2618．
13．在△ABC中，cos（A+B）=（　　）
A．cosCB．-cosCC．sinCD．-sinC
3．若数列{an}的通项公式an=$\frac{1}{2+4+6+…+2n}$，且前n项和为Sn，则S2015=（　　）
A．$\frac{2015}{2016}$B．$\frac{2014}{2015}$C．$\frac{4028}{2015}$D．$\frac{2014}{4030}$
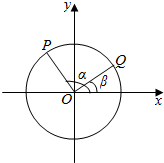10．如图，以x轴正半轴为始边作角α与β（0＜β＜α＜π），它们终边分别与单位圆相交于点P、Q．已知点P（-$\frac{3}{5}$，$\frac{4}{5}$），$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0，求：
（1）Q点坐标；
（2）sin（α+β）．
10．四棱锥P-ABCD中，底面ABCD是边长为a的菱形，∠A=60°，PC⊥平面ABCD，PC=a，E为PA的中点，
（1）求证：PC∥平面EBD．
（2）求E到平面PBC的距离．
11．若函数f（x）满足f′（x）-f（x）=2xex，f（0）=1，其中f′（x）为f（x）的导函数，则当x＞0时，$\frac{f′（x）}{f（x）}$的最大值为（　　）
A．$\sqrt{2}$B．2C．2$\sqrt{2}$D．4

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网