题目内容
10.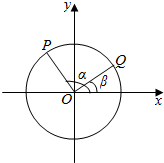 如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求:
如图,以x轴正半轴为始边作角α与β(0<β<α<π),它们终边分别与单位圆相交于点P、Q.已知点P(-$\frac{3}{5}$,$\frac{4}{5}$),$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,求:(1)Q点坐标;
(2)sin(α+β).
分析 (1)设Q点坐标为(x,y),根据向量的数量积为0,以及向量的模为1,即可求出x,y的值,
(2)由三角函数的定义,得出cosα、sinα,cosβ,sinβ,从而求出sin(α+β)的值.
解答  解:(1)∵P(-$\frac{3}{5}$,$\frac{4}{5}$),以x轴正半轴为始边作角α与β(0<β<α<π),
解:(1)∵P(-$\frac{3}{5}$,$\frac{4}{5}$),以x轴正半轴为始边作角α与β(0<β<α<π),
∴0<β<$\frac{π}{2}$,$\frac{π}{2}$<α<π
设Q点坐标为(x,y),
∵$\overrightarrow{OP}$•$\overrightarrow{OQ}$=0,P点在单位圆上,
∴-$\frac{3}{5}$x+$\frac{4}{5}$y=0,x2+y2=1,
解得x=$\frac{4}{5}$,y=$\frac{3}{5}$,
∴Q点坐标为($\frac{4}{5}$,$\frac{3}{5}$),
(2)P(-$\frac{3}{5}$,$\frac{4}{5}$),由三角函数的定义得,cosα=-$\frac{3}{5}$,sinα=$\frac{4}{5}$,
Q($\frac{4}{5}$,$\frac{3}{5}$),由三角函数的定义得,sinβ=$\frac{3}{5}$,cosβ=$\frac{4}{5}$,
∴sin(α+β)=sinαcosβ+cosαsinβ=$\frac{4}{5}×\frac{4}{5}$-$\frac{3}{5}$×$\frac{3}{5}$=$\frac{7}{25}$.
点评 本题考查了三角函数的求值与应用问题,解题时应根据三角函数的定义以及三角恒等公式进行计算,是基础题.

练习册系列答案
相关题目
20.设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是( )
| A. | 若m∥α,n∥β且α⊥β,则m⊥n | B. | 若m∥α,n∥β且α⊥β,则m∥n | ||
| C. | 若m⊥α,n∥m且α∥β,则m⊥n | D. | 若m∥α,n∥β且α∥β,则m∥n |
2.已知点E是正方形ABCD的边AD上一动点(端点除外),现将△ABE沿BE所在直线翻折成△A′BE,并连结A′C,A′D.记二面角A′-BE-C的大小为α(0<α<π).则( )
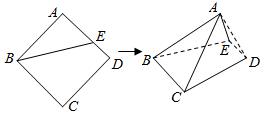

| A. | 存在α,使得BA′⊥面A′DE | B. | 存在α,使得BA′⊥面A′CD | ||
| C. | 存在α,使得EA′⊥面A′CD | D. | 存在α,使得EA′⊥面A′BC |
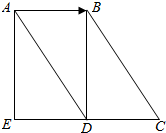 如图所示,四边形ABCD是平行四边形,四边形ABDE是矩形.
如图所示,四边形ABCD是平行四边形,四边形ABDE是矩形.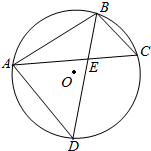 如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.
如图,圆O为△ABC的外接圆,D为$\widehat{AC}$的中点,BD交AC于E.