题目内容
9.已知sinαcosα=$\frac{1}{3}$,则sin2α=$\frac{2}{3}$cos4α=$\frac{1}{9}$.分析 使用二倍角公式计算.
解答 解:sin2α=2sinαcosα=$\frac{2}{3}$,cos4α=1-2sin22α=1-$\frac{8}{9}$=$\frac{1}{9}$.
故答案为$\frac{2}{3}$,$\frac{1}{9}$.
点评 本题考查了二倍角公式的应用,属于基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
20.设m,n是两条不同的直线,α,β是两个不同的平面,则下列结论正确的是( )
| A. | 若m∥α,n∥β且α⊥β,则m⊥n | B. | 若m∥α,n∥β且α⊥β,则m∥n | ||
| C. | 若m⊥α,n∥m且α∥β,则m⊥n | D. | 若m∥α,n∥β且α∥β,则m∥n |
2.已知点E是正方形ABCD的边AD上一动点(端点除外),现将△ABE沿BE所在直线翻折成△A′BE,并连结A′C,A′D.记二面角A′-BE-C的大小为α(0<α<π).则( )
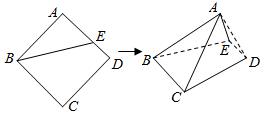

| A. | 存在α,使得BA′⊥面A′DE | B. | 存在α,使得BA′⊥面A′CD | ||
| C. | 存在α,使得EA′⊥面A′CD | D. | 存在α,使得EA′⊥面A′BC |
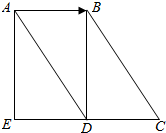 如图所示,四边形ABCD是平行四边形,四边形ABDE是矩形.
如图所示,四边形ABCD是平行四边形,四边形ABDE是矩形.