题目内容
11．若函数f（x）满足f′（x）-f（x）=2xex，f（0）=1，其中f′（x）为f（x）的导函数，则当x＞0时，$\frac{f′（x）}{f（x）}$的最大值为（ ）| A． | $\sqrt{2}$ | B． | 2 | C． | 2$\sqrt{2}$ | D． | 4 |
分析 利用函数f（x）满足f′（x）-f（x）=2xex，f（0）=1，求出f（x），再代入利用基本不等式即可得出结论．
解答 解：由题意，（$\frac{f（x）}{{e}^{x}}$）′=2x，
∴$\frac{f（x）}{{e}^{x}}$=x2+b，
∴f（x）=（x2+b）ex，
∵f（0）=1，∴b=1，
∴f（x）=（x2+1）ex，
f′（x）=（x+1）2ex，
∴当x＞0时，$\frac{f′（x）}{f（x）}$=1+$\frac{2x}{{x}^{2}+1}$≤2，当且仅当x=1时取等号，
∴当x＞0时，$\frac{f′（x）}{f（x）}$的最大值为2．
故选：B．
点评 本题考查导数知识的运用，考查基本不等式，考查学生的计算能力，确定f（x）是关键．
练习册系列答案
全能测控期末小状元系列答案
相关题目
2．已知点E是正方形ABCD的边AD上一动点（端点除外），现将△ABE沿BE所在直线翻折成△A′BE，并连结A′C，A′D．记二面角A′-BE-C的大小为α（0＜α＜π）．则（ ）
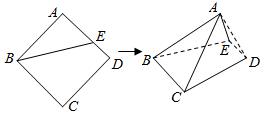
| A． | 存在α，使得BA′⊥面A′DE | B． | 存在α，使得BA′⊥面A′CD | ||
| C． | 存在α，使得EA′⊥面A′CD | D． | 存在α，使得EA′⊥面A′BC |
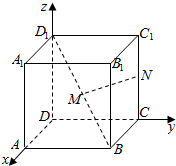如图所示，建立空间直角坐标系Dxyz，已知正方体ABCD-A1B1C1D1的棱长为1，点M是正方体对角线D1B的中点，点N在棱CC1上．
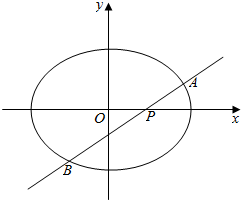椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（1，$\frac{\sqrt{2}}{2}$），且离心率为$\frac{\sqrt{2}}{2}$，过点P的动直线l与椭圆相交于A，B两点．
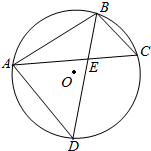如图，圆O为△ABC的外接圆，D为$\widehat{AC}$的中点，BD交AC于E．