题目内容
3．若数列{an}的通项公式an=$\frac{1}{2+4+6+…+2n}$，且前n项和为Sn，则S2015=（ ）| A． | $\frac{2015}{2016}$ | B． | $\frac{2014}{2015}$ | C． | $\frac{4028}{2015}$ | D． | $\frac{2014}{4030}$ |
分析 利用等差数列的前n项和公式、“裂项求和”方法即可得出．
解答 解：数列{an}的通项公式an=$\frac{1}{2+4+6+…+2n}$=$\frac{1}{\frac{n（2+2n）}{2}}$=$\frac{1}{n（n+1）}$=$\frac{1}{n}-\frac{1}{n+1}$，
则前n项和为Sn=$（1-\frac{1}{2}）$+$（\frac{1}{2}-\frac{1}{3}）$+…+$（\frac{1}{n}-\frac{1}{n+1}）$=1-$\frac{1}{n+1}$=$\frac{n}{n+1}$．
则S2015=$\frac{2015}{2016}$．
故选：A．
点评 本题考查了等差数列的前n项和公式、“裂项求和”方法，考查了变形能力与计算能力，属于中档题．
练习册系列答案
王后雄学案教材完全解读系列答案
相关题目
13．已知实数x、y满足不等式组$\left\{\begin{array}{l}{2x-y≤6}\\{x-y-2≥0}\\{x≥a}\end{array}\right.$，若z=3x+y的最小值是8，则实数a=（ ）
| A． | 2 | B． | -$\frac{2}{7}$ | C． | 14 | D． | $\frac{14}{5}$ |
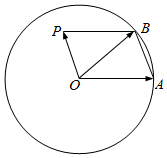已知点A、B为单位圆O上的两点，点P为单位圆0所在平面内的一点，且$\overrightarrow{OA}$与$\overrightarrow{OB}$不共线．
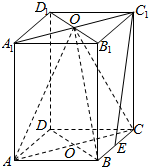如图，ABCD-A1B1C1D1是长方体，已知AA1=AC=2，AB=$\sqrt{2}$，O、O1分别是上下底面ABCD和A1B1C1D1的对角线的交点，E是BC的中点．
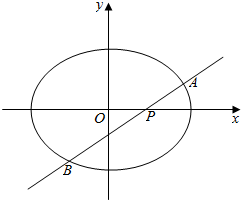椭圆E：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）经过点（1，$\frac{\sqrt{2}}{2}$），且离心率为$\frac{\sqrt{2}}{2}$，过点P的动直线l与椭圆相交于A，B两点．