题目内容
16.已知函数f(x)=1+x-$\frac{{x}^{2}}{2}$+$\frac{{x}^{3}}{3}$-$\frac{{x}^{4}}{4}$+…+$\frac{{x}^{2015}}{2015}$(x>-1),设F(x)=f(x-4),且函数F(x)的零点在区间[a-1,a](a∈Z)内,则${(x+\frac{a}{2})}^{a}$的展开式中x3的系数为( )| A. | 20 | B. | 15 | C. | 12 | D. | 8 |
分析 由题意可得f(0)=1,f(-1)<0,利用导数可得f(x)在(-1,0)上单调递增,f(x)在(-1,0)上有唯一零点,可得F(x)的零点所在的区间为(3,4),求得a=4.再利用二项展开式的通项公式求得${(x+\frac{a}{2})}^{a}$的展开式中x3的系数.
解答 解:由题意可得f(0)=1,f(-1)=1-1+(-$\frac{1}{2}$+$\frac{1}{3}$)+(-$\frac{1}{4}$+$\frac{1}{5}$)+…+(-$\frac{1}{2014}$+$\frac{1}{2015}$)<0,
f′(x)=1-x+x2-x3+…+-x2013+x2014 在(-1,0)上大于零,f(x)在(-1,0)上单调递增,
故f(x)在(-1,0)上有唯一零点.
F(x)=f(x-4)=f(x-4)-$\frac{{(x-4)}^{2}}{2}$+$\frac{{(x-4)}^{3}}{3}$-$\frac{{(x-4)}^{4}}{4}$+…+$\frac{{(x-4)}^{2015}}{2015}$的图象,是把f(x)的图象向右平移4个单位得到的,
故F(x)的零点所在的区间为(3,4).
再根据数F(x)的零点在区间[a-1,a],可得a=4,
故则${(x+\frac{a}{2})}^{a}$=(x+2)4,故则${(x+\frac{a}{2})}^{a}$的展开式中x3的系数为 ${C}_{4}^{1}$•2=8,
故选:D.
点评 本题主要考查利用导数研究函数的单调性,函数零点的判定定理,二项式定理的应用,二项展开式的通项公式,属于中档题.

练习册系列答案
 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案
相关题目
7.三个数a=0.67,b=70.6,c=log0.76的大小关系为( )
| A. | b<c<a | B. | b<a<c | C. | c<a<b | D. | c<b<a |
8.要得到函数y=sin$\frac{1}{2}$x的图象,只需将函数y=sin($\frac{1}{2}$x+$\frac{π}{4}$)的图象( )
| A. | 向左平移$\frac{π}{4}$个单位长度 | B. | 向右平移$\frac{π}{4}$个单位长度 | ||
| C. | 向左平移$\frac{π}{2}$个单位长度 | D. | 向右平移$\frac{π}{2}$个单位长度 |
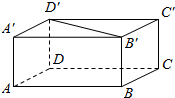 已知:如图的长方体AC′,求证:B′D′∥平面ABCD.
已知:如图的长方体AC′,求证:B′D′∥平面ABCD.