题目内容
5.画出函数y=|tanx|+tanx的图象,并根据图象求出函数的主要性质.分析 根据函数y的解析式,画出函数y的图象,结合图形求出它的定义域、值域和单调性、周期性即可.
解答 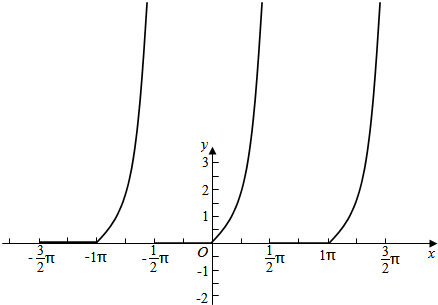 解:∵y=|tanx|+tanx=$\left\{\begin{array}{l}{2tanx,x∈[kπ,\frac{π}{2}+kπ),k∈Z}\\{0,x∈(-\frac{π}{2}+kπ,kπ),k∈Z}\end{array}\right.$,
解:∵y=|tanx|+tanx=$\left\{\begin{array}{l}{2tanx,x∈[kπ,\frac{π}{2}+kπ),k∈Z}\\{0,x∈(-\frac{π}{2}+kπ,kπ),k∈Z}\end{array}\right.$,
∴画出函数y=|tanx|+tanx的图象,如图所示;
则该函数的定义域是{x|x≠$\frac{π}{2}$+kπ,k∈z},
值域是[0,+∞),
单调递增区间是[kπ,kπ+$\frac{π}{2}$),k∈z,
最小正周期是π.
点评 本题考查了正切函数的图象与性质的应用问题,也考查了数形结合思想的应用问题,是基础题目.

练习册系列答案
相关题目
15.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面的4个图形中,能表示集合M到集合N的函数关系的有( )
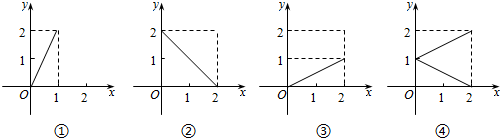
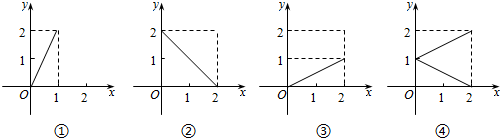
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
10.函数y=sin($\frac{π}{2}$-2015x)是( )
| A. | 奇函数 | B. | 偶函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |
14.若a=$\frac{ln3}{3}$、b=$\frac{1}{e}$、c=ln$\sqrt{2}$,则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |