题目内容
4.指出下列函数的最大值和最小值以及取得最值时x的值.(1)y=2sin($\frac{1}{3}x+\frac{π}{3}$);
(2)y=$\frac{1}{2}$sin(2x-$\frac{π}{4}$)
分析 根据振幅写出最值,令相位等于$\frac{π}{2}$+2kπ或-$\frac{π}{2}$+2kπ求出相应的x
解答 解:(1)最大值是2,最小值是-2.
令$\frac{1}{3}x+\frac{π}{3}$=$\frac{π}{2}$+2kπ,k∈Z,解得x=$\frac{π}{2}$+6kπ,k∈Z.
令$\frac{1}{3}x+\frac{π}{3}$=-$\frac{π}{2}$+2kπ,k∈Z,解得x=-$\frac{5π}{2}$+6kπ.k∈Z.
∴当x=$\frac{π}{2}$+6kπ时,k∈Z,y=2sin($\frac{1}{3}x+\frac{π}{3}$)取得最大值.
当x=-$\frac{5π}{2}$+6kπ时,k∈Z,y=2sin($\frac{1}{3}x+\frac{π}{3}$)取得最小值.
(2)最大值是$\frac{1}{2}$,最小值是-$\frac{1}{2}$.
令2x-$\frac{π}{4}$=$\frac{π}{2}$+2kπ,k∈Z,解得x=kπ+$\frac{3}{8}π$,k∈Z.
令2x-$\frac{π}{4}$=-$\frac{π}{2}$+2kπ,k∈Z,解得x=kπ-$\frac{π}{8}$,k∈Z.
∴当x=kπ+$\frac{3}{8}π$时,k∈Z,y=$\frac{1}{2}$sin(2x-$\frac{π}{4}$)取得最大值,
当x=kπ-$\frac{π}{8}$时,k∈Z,y=$\frac{1}{2}$sin(2x-$\frac{π}{4}$)取得最小值.
点评 本题考查了y=Asin(ωx+φ)的最值,是基础题.

练习册系列答案
相关题目
15.设集合M={x|0≤x≤2},N={y|0≤y≤2},那么下面的4个图形中,能表示集合M到集合N的函数关系的有( )
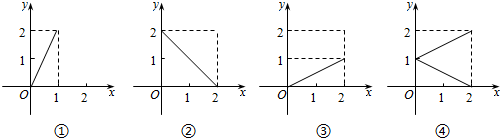
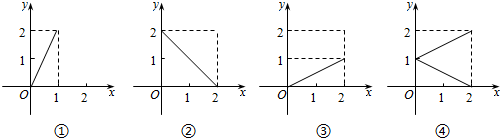
| A. | ①②③④ | B. | ①②③ | C. | ②③ | D. | ② |
14.若a=$\frac{ln3}{3}$、b=$\frac{1}{e}$、c=ln$\sqrt{2}$,则( )
| A. | a<b<c | B. | c<b<a | C. | c<a<b | D. | b<a<c |