题目内容
已知函数f(x),(x∈D),若同时满足以下条件:
①f(x)在D上单调递减或单调递增;
②存在区间[a,b]⊆D,使f(x)在[a,b]上的值域是[a,b](a<b).那么撑f(x)(x∈D)为闭函数.
(1)求闭函数f(x)=
符合条件②的区间[a,b];
(2)判断函数y=lnx+3x-6是不是闭函数,若是请找出区间[a,b],若不是请说明理由;
(3)若y=(x-k)2,x∈(k,+∞)是闭函数,求实数k的取值范围.
①f(x)在D上单调递减或单调递增;
②存在区间[a,b]⊆D,使f(x)在[a,b]上的值域是[a,b](a<b).那么撑f(x)(x∈D)为闭函数.
(1)求闭函数f(x)=
| x |
(2)判断函数y=lnx+3x-6是不是闭函数,若是请找出区间[a,b],若不是请说明理由;
(3)若y=(x-k)2,x∈(k,+∞)是闭函数,求实数k的取值范围.
考点:命题的真假判断与应用
专题:函数的性质及应用
分析:(1)根据函数f(x)=
为单调递增函数,可得
(a<b),解得答案;
(2)由函数lnx+3x-6在(0,+∞)单调递增可知
,结合对数函数的单调性可判断;
(3)由y=(x-k)2,x∈(k,+∞)是闭函数,易知函数是增函数,则在区间[a,b]上函数的值域也是[a,b],说明函数f(x)图象与直线y=x有两个不同交点,结合函数的图象可求实数k的取值范围.
| x |
|
(2)由函数lnx+3x-6在(0,+∞)单调递增可知
|
(3)由y=(x-k)2,x∈(k,+∞)是闭函数,易知函数是增函数,则在区间[a,b]上函数的值域也是[a,b],说明函数f(x)图象与直线y=x有两个不同交点,结合函数的图象可求实数k的取值范围.
解答:
解:(1)∵函数f(x)=
在[0,+∞)上为单调递增函数,
若存在区间[a,b]⊆D,使f(x)在[a,b]上的值域是[a,b],
则
(a<b),
即a,b为
=x的两个非负根,
解
=x得:x=0,或x=1,
∴a=0,b=1;
(2)∵函数lnx+3x-6在(0,+∞)单调递增,
若函数y=lnx+3x-6是闭函数,
则
,
即a,b为lnx=6-2x的两个正根,
由方程lnx=6-2x有且只有一个正根,
故函数y=lnx+3x-6不是闭函数;
(3)若y=(x-k)2,x∈(k,+∞)是闭函数,
由y=(x-k)2,x∈(k,+∞)为增函数,
则
,
即a,b为x2-(2k+1)x+k2=0的两个大于k的根,
即
,
解得:k∈(-
,0)
| x |
若存在区间[a,b]⊆D,使f(x)在[a,b]上的值域是[a,b],
则
|
即a,b为
| x |
解
| x |
∴a=0,b=1;
(2)∵函数lnx+3x-6在(0,+∞)单调递增,
若函数y=lnx+3x-6是闭函数,
则
|
即a,b为lnx=6-2x的两个正根,
由方程lnx=6-2x有且只有一个正根,
故函数y=lnx+3x-6不是闭函数;
(3)若y=(x-k)2,x∈(k,+∞)是闭函数,
由y=(x-k)2,x∈(k,+∞)为增函数,
则
|
即a,b为x2-(2k+1)x+k2=0的两个大于k的根,
即
|
解得:k∈(-
| 1 |
| 4 |
点评:本题主要考查了函数的单调性的综合应用,方程的解与函数的交点的相互转化关系的应用,综合应用了函数的知识及数形结合思想、转化思想.

练习册系列答案
相关题目
设a=log23.9,b=log20.7,c=2,则( )
| A、b<a<c |
| B、a<b<c |
| C、c<a<b |
| D、c<b<a |
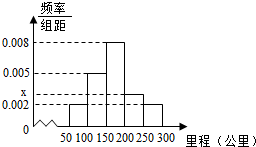 某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.
某校研究性学习小组从汽车市场上随机抽取20辆纯电动汽车调查其续驶里程(单次充电后能行驶的最大里程),被调查汽车的续驶里程全部介于50公里和300公里之间,将统计结果分成5组:[50,100),[100,150),[150,200),[200,250),[250,300),绘制成如图所示的频率分布直方图.