题目内容

已知函数f（x）=
1
3
|x|，判断并证明f（x）的奇偶性．
考点：函数奇偶性的判断
专题：函数的性质及应用
分析：先求出函数的定义域，判断是否关于原点对称，再化简f（-x）判断与f（x）的关系，最后根据函数的奇偶性下结论．
解答： 解：函数f（x）是偶函数，
证明如下：f（x）=
1
3
|x|的定义域是R，
且f（-x）=
1
3
|-x|=
1
3
|x|=f（x），
所以函数f（x）是偶函数．
点评：本题考查了函数的奇偶性的证明，需要先求定义域再判断f（-x）与f（x）的关系，属于基础题．
练习册系列答案
相关题目
已知不等式组
x-y-1≤0
x+y-2≥0
x＞0
，求：
（1）z=x2+y2的最小值；
（2）u=
y
x
的取值范围；
（3）u=|2x+y+1|的最小值；
（4）m=x-y的最大值．
已知函数f（x）=（a-1）
3-ax
在（0，1]上为减函数，求a的取值范围．
某工厂某种产品的年固定成本为250万元，每生产x千件，需另投入成本为A，当年产量不足80千件时，C（x）=
1
3
x2+10x（万元）．当年产量不小于80千件时，C（x）=51x+
10000
x
-1450（万元）．每件商品售价为0.05万元．通过市场分析，该厂生产的商品能全部售完．
（Ⅰ）写出年利润L（x）（万元）关于年产量x（千件）的函数解析式；
（Ⅱ）年产量为多少千件时，该厂在这一商品的生产中所获利润最大？
已知a，b为正实数，若函数f（x）=ax3+bx+ab-1是奇函数，则f（2）的最小值为
 
．
求焦点在坐标轴上，焦距为2
2
，且经过点（-
10
5
，
3
5
5
）的椭圆的标准方程．
已知函数f（x）=x2+2（a-2）x+5．
（1）若函数f（x）在（4，+∞）上单调递增，求实数a的取值范围；  
（2）若f（-1）=8，求函数f（x）在[0，3]上的最值，并写出f（x）的单调区间．
已知cosα+2sinα=0，其中
π
2
＜α＜π．
（Ⅰ）求
sinα-2cosα
2sinα-cosα
的值；
（Ⅱ）若sinβ=
3
5
，
π
2
＜β＜π，求cos﹙α+β﹚的值．
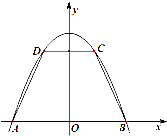如图，抛物线y=-x2+9与x轴交于两点A，B，点C，D在抛物线上（点C在第一象限），CD∥AB．记|CD|=2x，梯形ABCD面积为S．
（1）求面积S以x为自变量的函数式；
（2）若
|CD|
|AB|
=k其中k为常数，且0＜k＜1，求S的最大值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网