题目内容
已知cosα+2sinα=0,其中
<α<π.
(Ⅰ)求
的值;
(Ⅱ)若sinβ=
,
<β<π,求cos﹙α+β﹚的值.
| π |
| 2 |
(Ⅰ)求
| sinα-2cosα |
| 2sinα-cosα |
(Ⅱ)若sinβ=
| 3 |
| 5 |
| π |
| 2 |
考点:两角和与差的余弦函数,三角函数的化简求值
专题:三角函数的求值
分析:(Ⅰ)求出正切函数值,所求
化为正切函数的形式,运算求得结果.
(Ⅱ)利用已知条件求出sinα,cosα,以及sinβ,然后利用两角和的余弦函数求解即可.
| sinα-2cosα |
| 2sinα-cosα |
(Ⅱ)利用已知条件求出sinα,cosα,以及sinβ,然后利用两角和的余弦函数求解即可.
解答:
解:(Ⅰ)由于cosα+2sinα=0,tanα=-
,∴
=
=
=
,
(Ⅱ)sinβ=
,
<β<π,∴cosβ=-
,
cosα+2sinα=0,其中
<α<π.
又cos2α+sin2α=1,∴cosα=-
,sinα=
.
∴cos﹙α+β﹚=-
×(-
)-
×
=
.
| 1 |
| 2 |
| sinα-2cosα |
| 2sinα-cosα |
| tanα-2 |
| 2tanα-1 |
-
| ||
2×(-
|
| 5 |
| 4 |
(Ⅱ)sinβ=
| 3 |
| 5 |
| π |
| 2 |
| 4 |
| 5 |
cosα+2sinα=0,其中
| π |
| 2 |
又cos2α+sin2α=1,∴cosα=-
2
| ||
| 5 |
| ||
| 5 |
∴cos﹙α+β﹚=-
2
| ||
| 5 |
| 4 |
| 5 |
| 3 |
| 5 |
| ||
| 5 |
| ||
| 5 |
点评:本题主要考查同角三角函数的基本关系的应用,两角和与差的三角函数,基本知识的考查属.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
下列关于函数f(x)=(x+1)|x|的单调性的叙述中,正确的是( )
| A、f(x)在定义域上单调递增 | ||
| B、f(x)在定义域上单调递减 | ||
| C、f(x)在(-∞,0)上是增函数,在(0,+∞)上是减函数 | ||
D、f(x)在(-
|
当a>0时,函数f(x)=(x2-ax)ex的图象大致是( )
A、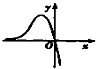 |
B、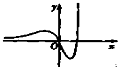 |
C、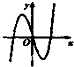 |
D、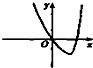 |