题目内容
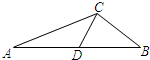如图，在△ABC中，|| AB |
| AC |
| BC |
| BA |
| CA |
| CB |
（1）求C的大小；
（2）设D为AB的中点，求CD的长．
考点：余弦定理
专题：三角函数的求值,解三角形
分析：（1）根据已知求出BC，CA与AB的长，利用余弦定理表示出cosC，将三边长代入求出cosC的值，即可确定出C的度数；
（2）利用余弦定理求出cosA的值，在三角形ADC中，求出AD的长，利用余弦定理即可求出CD的长．
（2）利用余弦定理求出cosA的值，在三角形ADC中，求出AD的长，利用余弦定理即可求出CD的长．
解答：
解：（1）依题意BC=3，CA=5，AB=7，
由余弦定理，得cosC=
=-
，
∵0＜C＜π，
∴C=
；
（2）由余弦定理，得cosA=
=
，
在△ADC中，AD=
，
根据余弦定理得：CD2=AC2+AD2-2AC×AD×cosA=
，
则CD=
．
由余弦定理，得cosC=
| CB2+CA2-AB2 |
| 2CB•CA |
| 1 |
| 2 |
∵0＜C＜π，
∴C=
| 2π |
| 3 |
（2）由余弦定理，得cosA=
| CA2+AB2-BC2 |
| 2CA•AB |
| 13 |
| 14 |
在△ADC中，AD=
| 7 |
| 2 |
根据余弦定理得：CD2=AC2+AD2-2AC×AD×cosA=
| 19 |
| 4 |
则CD=
| ||
| 2 |
点评：此题考查了余弦定理，以及特殊角的三角函数值，熟练掌握余弦定理是解本题的关键．
练习册系列答案
相关题目
平面上动点A（x，y）满足
+
=1，B（-4，0），C（4，0），则一定有（ ）
| |x| |
| 5 |
| |y| |
| 3 |
| A、|AB|+|AC|＜10 |
| B、|AB|+|AC|≤10 |
| C、|AB|+|AC|＞10 |
| D、|AB|+|AC|≥10 |
某商场分别投入x万元，经销甲、乙两种商品，可分别获得利润y1、y2万元，利润曲线分别为C1：y1=m•ax+b，C2：y2=cx，其中m，a，b，c都为常数．如图所示：