题目内容
18.某班级50名学生的考试分数x分布在区间[50,100)内,设分数x的分布频率是f(x)且f(x)=$\left\{\begin{array}{l}{\frac{n}{10}-0.4,10n≤x<10(n+1),n=5,6,7}\\{-\frac{n}{5}+b,10n≤x<10(n+1),n=8,9}\end{array}\right.$,考试成绩采用“5分制”,规定:考试分数在[50,60)内的成绩记为1分,考试分数在[60,70)内的成绩记为2分,考试分数在[70,80)内的成绩记为3分,考试分数在[80,90)内的成绩记为4分,考试分数在[90,100)内的成绩记为5分.用分层抽样的方法,现在从成绩在1分,2分及3分的人中用分层抽样随机抽出6人,再从这6人中抽出3人,记这3人的成绩之和为ξ(将频率视为概率).(1)求b的值,并估计班级的考试平均分数;
(2)求P(ξ=7);
(3)求ξ的分布列和数学期望.
分析 (1)求出各个分数段的频率,列出频率分布表,根据频率之和为1,求得b,再求平均值.
(2)从成绩在1分,2分及3分的人中用分层抽样随机抽出6人,则成绩为1分、2分、3分的分别为1人、2人、3人,再从这6人中抽出3人,成绩之和为7的情况有,1+3+3,2+2+3
(3)ξ的可能取值为5,6,7,8,9,求出相应概率,再求解.
解答 解:(1)依题意频率分布表如下:
| 分数 | [50,60) | [60.70) | [70.80) | [80,90) | [90,100) |
| 成绩 | 1 | 2 | 3 | 4 | 5 |
| 频率 | 0.1 | 0.2 | 0.3 | b-1.6 | b-1.8 |
班级的平均成绩$\overline{x}$=55×0.1+65×0.2+75×0.3+85×0.3+95×0.1=76(分)
(2)从成绩在1分,2分及3分的人中用分层抽样随机抽出6人,则成绩为1分、2分、3分的分别为1人、2人、3人,
再从这6人中抽出3人,记这3人的成绩之和为ξ,P(ξ=7)=$\frac{1{×C}_{3}^{2}+1{×C}_{3}^{1}}{{C}_{6}^{3}}=\frac{6}{20}=\frac{3}{10}$
(3)ξ的可能取值为5,6,7,8,9
P(ξ=5)=$\frac{1}{20}$,P(ξ=6)=$\frac{6}{20}$,P(ξ=7)=$\frac{6}{20}$,P(ξ=8)=$\frac{6}{20}$,P(ξ=9)=$\frac{1}{20}$
ξ的分布列如下:
| ξ | 5 | 6 | 7 | 8 | 9 |
| P | $\frac{1}{20}$ | $\frac{6}{20}$ | $\frac{6}{20}$ | $\frac{6}{20}$ | $\frac{1}{20}$ |
点评 本题考查了抽样方法、统计的初步知识,及离散型随机变量的分布列、数学期望,属于中档题.

练习册系列答案
相关题目
10.若函数f(x)=x2-4x+a对于一切x∈[0,1]时,恒有f(x)≥0成立,则实数a的取值范围是( )
| A. | [3,+∞) | B. | (3,+∞) | C. | (-∞,3] | D. | (-∞,3) |
8.若a为实数,i为虚数单位,且$\frac{2+ai}{1+i}=3+i$,则a=( )
| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
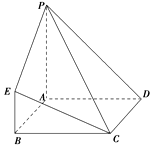 在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.