题目内容
13.有三个数成等差数列,前两个数的和的3倍正好是第三个数的2倍,如果把第二个数减去2,那么所得数是第一个数与第三个数的等比中项.求原来的三个数.分析 设成等差数列的三个数分别为a-d,a,a+d,运用等比数列的中项的性质,结合条件可得a,d的方程,解方程,即可得到所求三个数.
解答 解:设成等差数列的三个数分别为a-d,a,a+d,
由题意,得$\left\{\begin{array}{l}3(2a-d)=2(a+d)\\(a-d)(a+d)={(a-2)^2}\end{array}\right.$
即$\left\{\begin{array}{l}4a=5d\\ 4a={d^2}+4\end{array}\right.$,
解得,$\left\{\begin{array}{l}d=4\\ a=5\end{array}\right.$或$\left\{\begin{array}{l}d=1\\ a=\frac{5}{4}\end{array}\right.$,
所以,原来的三个数分别为1,5,9或$\frac{1}{4},\frac{5}{4},\frac{9}{4}$.
点评 本题考查等差数列通项公式的运用,注意设出等差数列中连续的三个数,考查方程思想和运算求解能力,属于基础题.

练习册系列答案
 小题狂做系列答案
小题狂做系列答案
相关题目
5.已知A,B分别为椭圆C:$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)$的左、右顶点,不同两点P,Q在椭圆C上,且关于x轴对称,设直线AP,BQ的斜率分别为m,n,则当$\frac{a}{b}+3\sqrt{mn}$取最小值时,椭圆C的离心率为( )
| A. | $\frac{{\sqrt{2}}}{3}$ | B. | $\frac{{\sqrt{3}}}{3}$ | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{6}}}{3}$ |
3.已知复数z满足($\sqrt{3}$+3i)z=$\sqrt{3}$i,则z=( )
| A. | $\frac{{\sqrt{3}}}{4}+\frac{1}{4}i$ | B. | $\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ | C. | $\frac{{\sqrt{3}}}{4}-\frac{1}{4}i$ | D. | $\frac{1}{4}-\frac{{\sqrt{3}}}{4}i$ |
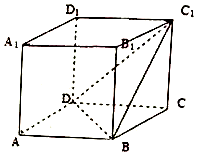 在直四棱柱ABCD-A1B1C1D1中,AB=4,AA1=2$\sqrt{3}$,底面ABCD为菱形,且∠BAD=60°.
在直四棱柱ABCD-A1B1C1D1中,AB=4,AA1=2$\sqrt{3}$,底面ABCD为菱形,且∠BAD=60°.