题目内容
3.已知函数g(x)=$\frac{1}{xsinθ}$+lnx在[1,+∞)上为增函数,且θ∈(0,π),f(x)=mx-$\frac{m-1}{x}$-lnx(m∈R).(1)求θ的值;
(2)设h(x)=$\frac{2e}{x}$,若在[1,e]上至少存在一个x0,使得f(x0)-g(x0)>h(x0)成立,求m的取值范围.
分析 (1)由题意可知$\frac{sinθ•x-1}{sinθ{•x}^{2}}$≥0.由θ∈(0,π),知sinθ>0.再由sinθ≥1,结合θ∈(0,π),可以得到θ的值.
(2)构造F(x)=f(x)-g(x)-h(x),F(x)=mx-$\frac{m}{x}$-2lnx-$\frac{2e}{x}$,由此入手可以得到m的取值范围是( $\frac{4e}{{e}^{2}-1}$,+∞)
解答 解:(1)由题意,g′(x)=-$\frac{1}{sinθ{•x}^{2}}$+$\frac{1}{x}$≥0在[1,+∞)上恒成立,即$\frac{sinθ•x-1}{sinθ{•x}^{2}}$≥0.
∵θ∈(0,π),∴sinθ>0.故sinθ•x-1≥0在[1,+∞)上恒成立,只须sinθ•1-1≥0,
即sinθ≥1,只有sinθ=1.结合θ∈(0,π),得θ=$\frac{π}{2}$,
(2)构造F(x)=f(x)-g(x)-h(x),F(x)=mx-$\frac{m}{x}$-2lnx-$\frac{2e}{x}$,
当m≤0时,x∈[1,e],mx-$\frac{m}{x}$≤0,-2lnx-$\frac{2e}{x}$<0,
所以在[1,e]上不存在一个x0,使得f(x0)-g(x0)>h(x0)成立.
当m>0时,F′(x)=$\frac{{mx}^{2}-2x+m+2e}{{x}^{2}}$,
因为x∈[1,e],所以2e-2x≥0,mx2+m>0,
所以(F(x))'>0在x∈[1,e]恒成立.
故F(x)在[1,e]上单调递增,F(x)max=F(e)=me-$\frac{m}{e}$-4,只要me-$\frac{m}{e}$-4>0,
解得:m>$\frac{4e}{{e}^{2}-1}$,
故m的取值范围是:($\frac{4e}{{e}^{2}-1}$,+∞).
点评 本题考查函数的性质和应用,解题时要认真审题,注意挖掘隐含条件,仔细解答.

 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案 如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成的角的正弦值为( )
如图,在长方体ABCD-A1B1C1D1中,AB=BC=2,AA1=1,则AC1与平面A1B1C1D1所成的角的正弦值为( )| A. | $\frac{1}{3}$ | B. | $\frac{{2\sqrt{2}}}{3}$ | C. | $\frac{2}{3}$ | D. | $\frac{{\sqrt{2}}}{4}$ |
| A. | 3 | B. | $\frac{{5\sqrt{15}}}{3}$或$\sqrt{15}$ | C. | $\sqrt{5}$ | D. | $\frac{25}{3}$或3 |
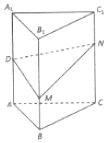 如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.
如图,正三棱柱ABC-A1B1C1的各棱长均相等,D为AA1的中点,M,N分别是线段BB1和线段CC1上的动点(含端点),且满足BM=C1N,当M,N运动时,下列结论中正确的序号为②③④.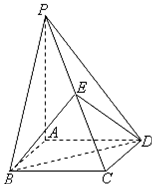 如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,E为PC中点.求证:平面BED⊥平面ABCD.
如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,E为PC中点.求证:平面BED⊥平面ABCD.