题目内容
8.若a为实数,i为虚数单位,且$\frac{2+ai}{1+i}=3+i$,则a=( )| A. | -4 | B. | -3 | C. | 3 | D. | 4 |
分析 利用复数的运算法则、复数相等即可得出.
解答 解:∵$\frac{2+ai}{1+i}=3+i$,∴2+ai=(1+i)(3+i)=2+4i,
则a=4.
故选:D.
点评 本题考查了复数的运算法则、复数相等,考查了推理能力与计算能力,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.已知复数z满足($\sqrt{3}$+3i)z=$\sqrt{3}$i,则z=( )
| A. | $\frac{{\sqrt{3}}}{4}+\frac{1}{4}i$ | B. | $\frac{1}{4}+\frac{{\sqrt{3}}}{4}i$ | C. | $\frac{{\sqrt{3}}}{4}-\frac{1}{4}i$ | D. | $\frac{1}{4}-\frac{{\sqrt{3}}}{4}i$ |
20.已知数列-3,7,-11,15…,则下列选项能表示数列的一个通项公式的是( )
| A. | an=4n-7 | B. | an=(-1)n(4n+1) | C. | an=(-1)n•(4n-1) | D. | an=(-1)n+1•(4n-1) |
17.已知函数f(x)是R上的偶函数,满足f(x)=-f(x+1),当x∈[2015,2016]时,f(x)=x-2017,则( )
| A. | $f(sin\frac{π}{3})>f(cos\frac{π}{3})$ | B. | f(sin2)>f(cos2) | C. | $f(sin\frac{π}{5})<f(cos\frac{π}{5})$ | D. | f(sin1)<f(cos1) |
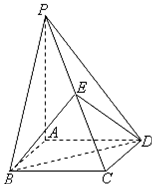 如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,E为PC中点.求证:平面BED⊥平面ABCD.
如图,四边形ABCD是边长为2的菱形,∠ABC=60°,PA⊥平面ABCD,E为PC中点.求证:平面BED⊥平面ABCD.