Question

（理）如图，在直三棱柱ABC-A₁B₁C₁中，AB⊥AC，AA₁=AB=AC=1，∠ABC=

π

4

，D、M、N分别是CC₁、A₁B₁、BC的中点．
（1）求异面直线MN与AC所成角的大小；
（2）求点M到平面ADN之间的距离．

Answer 1

考点：点、线、面间的距离计算,异面直线及其所成的角

专题：综合题,空间位置关系与距离,空间角

分析：（1）设AB的中点为E，连接EN，证明∠MNE或其补角即为异面直线MN与AC所成的角，连接ME，在Rt△MEN中，可求异面直线MN与AC所成角的大小；
（2）建立空间直角坐标系A-xyz，求出平面ADN的一个法向量，即可求点M到平面ADN之间的距离．

解答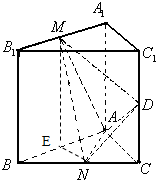： 解：（1）设AB的中点为E，连接EN，
则EN∥AC，且EN=

1

2

AC，
所以∠MNE或其补角即为异面直线MN与AC所成的角．…3分
连接ME，在Rt△MEN中，tan∠MNE=

ME

NE

=2…5分
所以异面直线MN与AC所成的角为arctan2．…6分
（2）因为AB=AC=1，∠ABC=

π

4

，所以AB⊥AC，
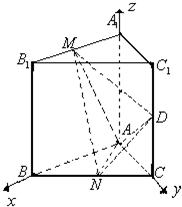
以点A为坐标原点，分别以AB、AC、AA₁所在直线为x，y，z轴，如图建立空间直角坐标系A-xyz，则：M(

1

2

，0，1)，N(

1

2

，

1

2

，0)，D(0，1，

1

2

)，…8分
设平面AND的一个法向量为

n

=(x，y，z)

则

n • AN =0 n • AD =0

⇒

x+y=0 y+ z 2 =0

所以平面ADN的一个法向量为

n

=(1，-1，2)．…10分
又

AM

=(

1

2

，0，1)，
所以点M到平面OAD的距离d=

| AM • n |

| n |

=

| 1 2 +2|

6

=

5 6

12

．…12分．

点评：本题考查异面直线所成角的大小、考查点M到平面ADN之间的距离，考查向量知识的运用，考查学生的计算能力，属于中档题．