题目内容

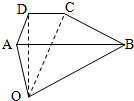如图，梯形ABCD中AB∥CD，AB=2CD，点O为空间任意一点，设
OA
=
a
，
OB
=
b
，
OC
=
c
，则向量
OD
用
a
，
b
，
c
表示为（　　）
A、
a
-
b
+2
c
B、
a
-
b
-2
c
C、-
1
2
a
+
1
2
b
+
c
D、
1
2
a
-
1
2
b
+
c
考点：平面向量的基本定理及其意义
专题：平面向量及应用
分析：易知
CD
=
1
2
BA
，由向量加法法则可得
OD
=
OA
+
AC
+
CD
=
OA
+
OC
-
OA
+
1
2
BA
，从而可得答案．
解答： 解：因为AB∥CD，AB=2CD，所以
CD
=
1
2
BA
，
OD
=
OA
+
AC
+
CD

=
OA
+
OC
-
OA
+
1
2
BA

=
OC
+
1
2
(
OA
-
OB
)=
1
2
a
-
1
2
b
+
c
，
故选D．
点评：本题考查平面向量的基本定理及其意义，属基础题．
练习册系列答案
相关题目
若函数f（x）=x3-3x+a有两个不同的零点，则实数a的取值是
 
．
已知函数f（x）=ax2+2x+c（a，c∈N）满足①f（1）=5；②6＜f（2）＜11
（1）求f（x）的解析式；
（2）若对任意实数x∈[
1
2
，
3
2
]，都有f（x）-2m≤1成立，求实数m的取值范围．
已知实数x，y满足不等式
2x-y≥0
x+y-4≥0
x≤3
，则
2x3+y3
x2y
的取值范围是
 
．
若曲线y=2x2的一条切线l与直线x+4y-8=0垂直，则切线l的方程为
 
．
在三棱锥A-BCD中，AB⊥AC，AB⊥AD，AC⊥AD，AB=AC=1，AD=2，E、F分别是BC、BD的中点．
（1）求证：BC⊥面AED；
（2）求A到面BCD的距离；
（3）求二面角C-AE-F的大小．
（1）已知圆C的参数方程为
x=cosα
y=1+sinα
（α为参数），以原点为极点，x轴正半轴为极轴建立极坐标系，直线l的极坐标方程为ρsinθ=1，（ρ≥0，0≤θ＜2π）则直线l与圆C的交点的极坐标为
 
．
（2）已知f（x）=|x|+|x-1|，若g（x）=f（x）-a的零点个数不为0，则a的最小值为
 
．
已知函数f（x）=x2-4sinθ•x-1，x∈[-1，
3
]，其中θ∈[0，2π]
（1）当θ=
π
6
时，求函数f（x）的最大最小值；
（2）求θ的取值范围，使y=f（x）在区间[-1，
3
]上存在反函数．
已知
i
，
j
是互相垂直的单位向量，设
a
=4
i
+3
j
，
b
=3
i
-4
j
，则 
a
•
b
=
 
．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网